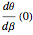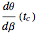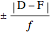Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Motion/Pursuit Law in 2D (Visual Depth Perception 3)

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

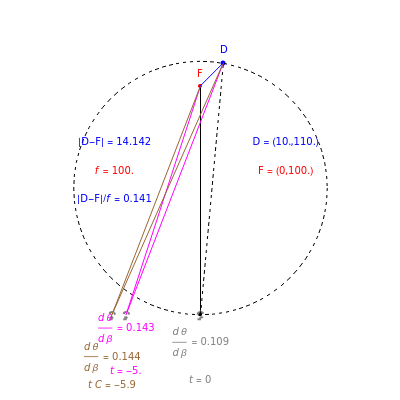
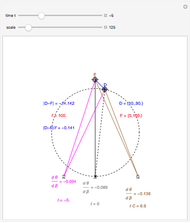
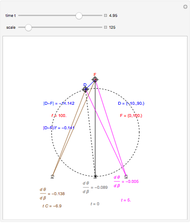
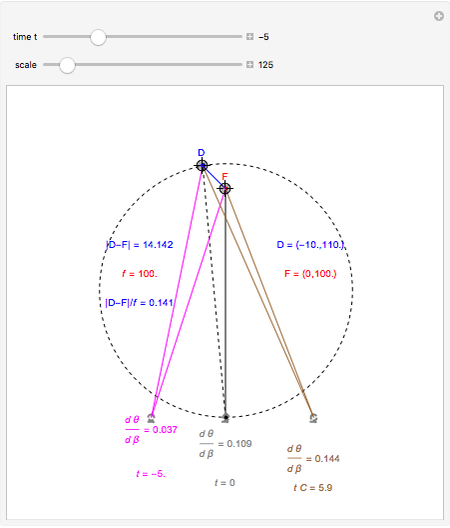
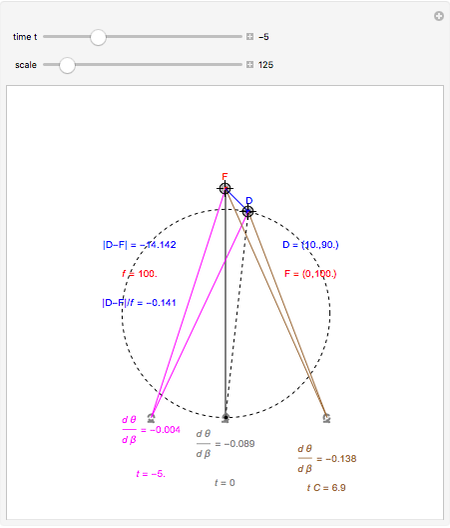
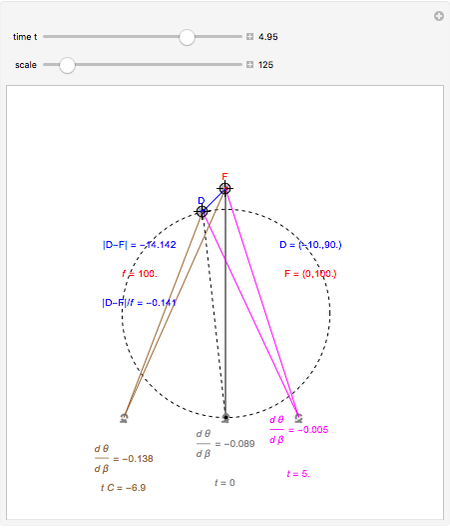
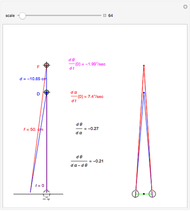
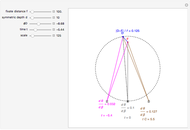
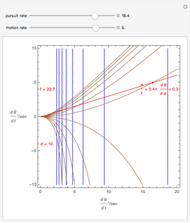
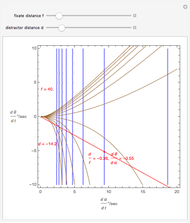
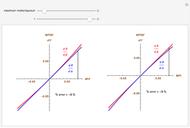
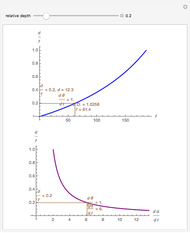
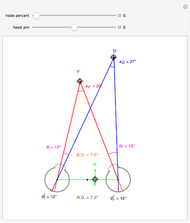
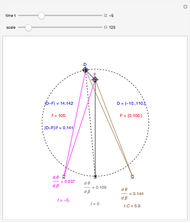
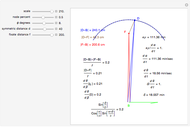
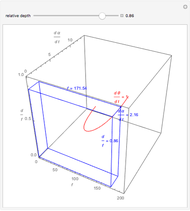
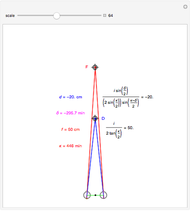
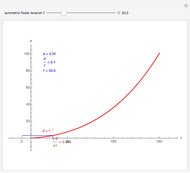
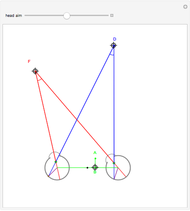
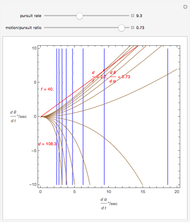
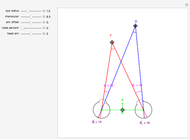
This Demonstration computes the motion/pursuit law in the two-dimensional horizontal fixation plane of the eyes. The observer is looking mainly at F on the vertical axis, but also sees D as he translates to the right at speed equal to the interocular distance per second.

[more]

We do not know a theoretical explanation for the rough approximation of the peak motion pursuit law by the 2D relative distance, but this Demonstration compares , , and the 2D signed relative distance, . It also lets you vary time and compare the motion/pursuit law at other times. You can drag the distractor point and the fixate distance is variable.

[less]

Contributed by: Keith Stroyan (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send