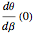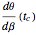Motion/Pursuit Law on Invariant Circles (Visual Depth Perception 4)

Initializing live version

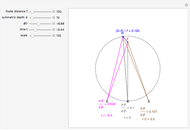
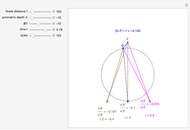
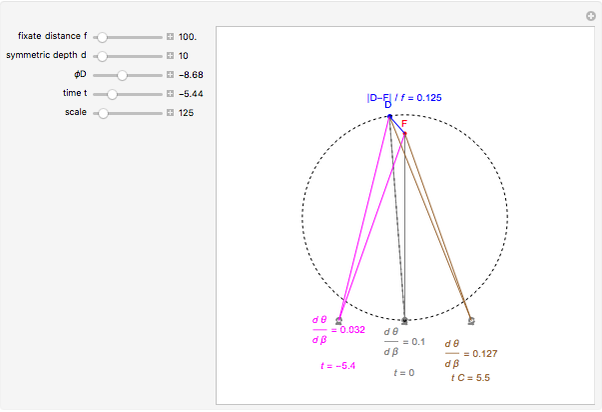
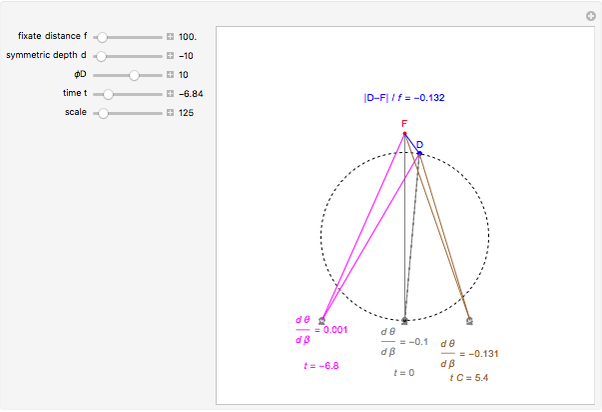
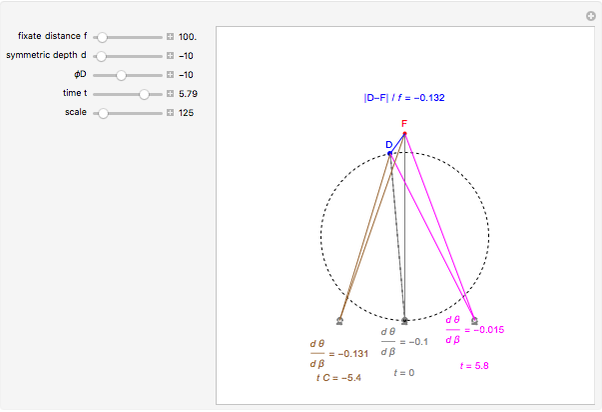
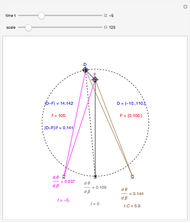
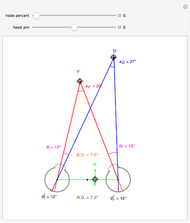
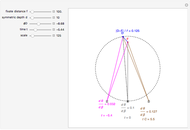
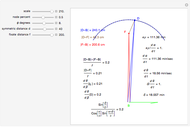
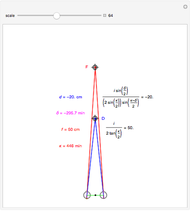
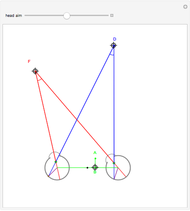
This Demonstration computes the motion/pursuit law in the two-dimensional horizontal "fixation plane" of the eyes. The observer is looking mainly at F on the vertical axis, but also sees D as she translates to the right at 6.5 cm/sec (interocular distance per second). The distractor can be moved off the axis around the time zero invariant circle.

[more]

Contributed by: Keith Stroyan (March 2011)
Open content licensed under CC BY-NC-SA

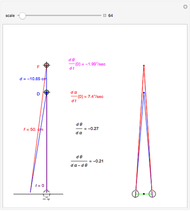
Snapshots

Details

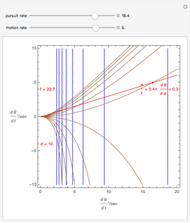
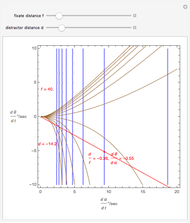
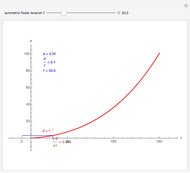
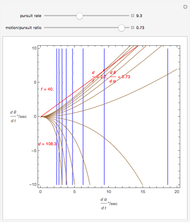
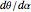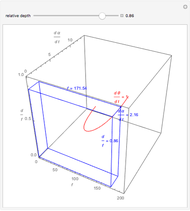
The motion/pursuit ratio at is constant on circles passing through the eye node at time zero and distractor 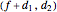with diameter on the axis. (These circles are similar to the invariant circles for binocular disparity, but slightly different.)

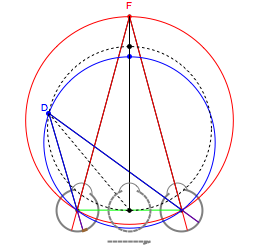
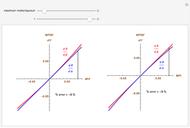
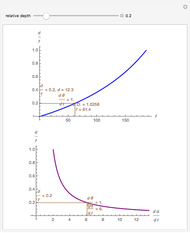
This means that the time zero motion/pursuit law is NOT an especially good indicator of the relative distance between the two-dimensional distractor and fixate, 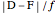, because you can move quite far from F on this circle with no change in the quantity . If we take the translation of the observer into account, we can show that the peak value of the motion/pursuit law is a good indicator of the relative distance in two dimensions. (It is also likely that the changing value of the motion/pursuit ratio is a cue that the brain could use.)

The Demonstration, "Motion/Pursuit Law in 2D (Visual Depth Perception 3)" (see Related Links) contains additional details.

Permanent Citation

Keith Stroyan "Motion/Pursuit Law on Invariant Circles (Visual Depth Perception 4)"
http://demonstrations.wolfram.com/MotionPursuitLawOnInvariantCirclesVisualDepthPerception4/
Wolfram Demonstrations Project
Published: March 7 2011


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send