Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Motion Parallax versus Depth, 2D (Visual Depth Perception 12)

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

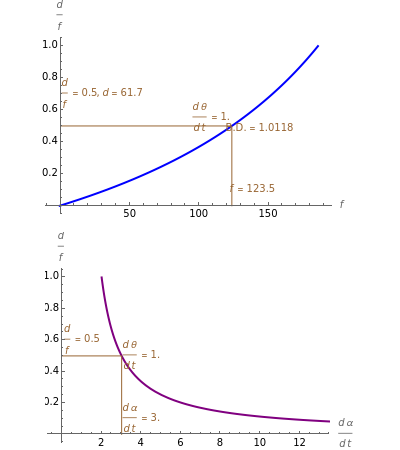
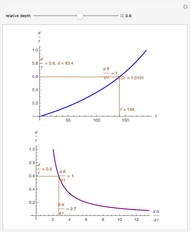
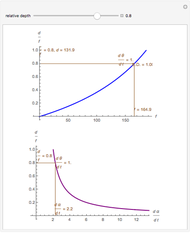
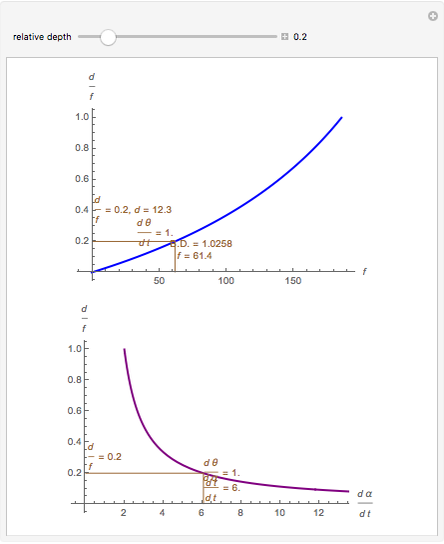
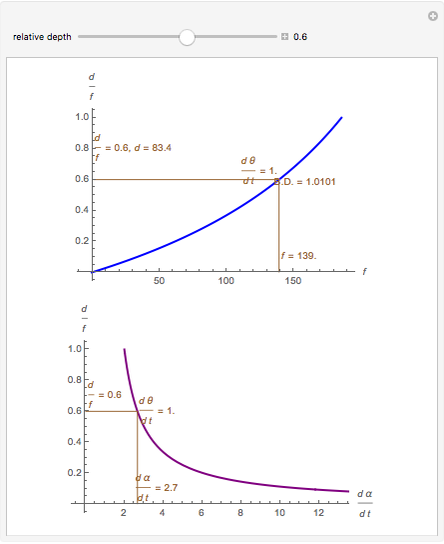
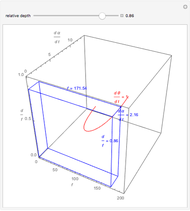
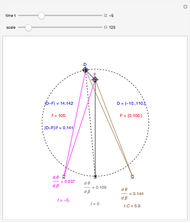
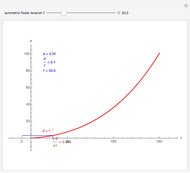
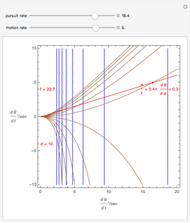
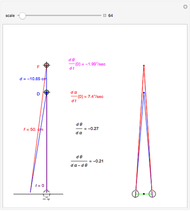
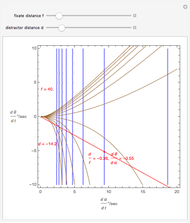
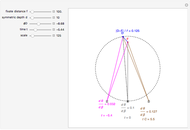
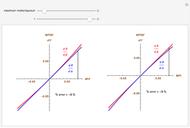
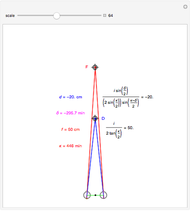
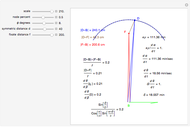
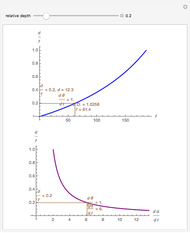
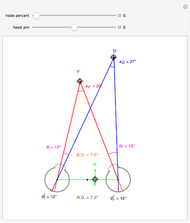
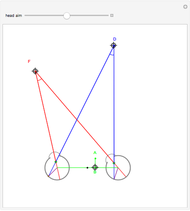
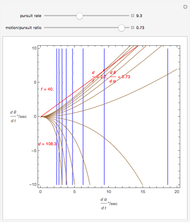
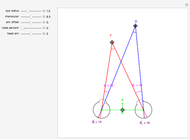
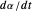This Demonstration lets you move the relative distance between and and uses the formulas below to find the fixate distance and pursuit rate , keeping the motion .

[more]

The program computes the binocular disparity of a fixed observer at the position. Notice that .

[less]

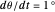Contributed by: Keith Stroyan (March 2011)
Open content licensed under CC BY-NC-SA

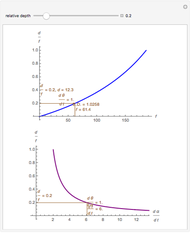
Snapshots

Details

$Failed
Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send