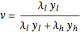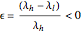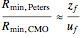Distillation of Substances with Widely Differing Heats of Vaporization: The Peters Transform

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
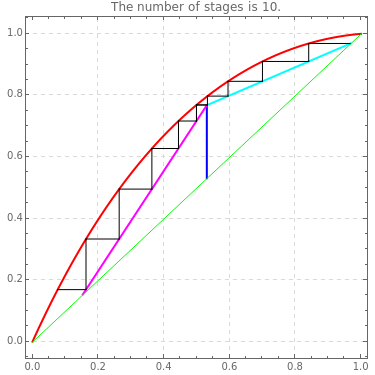
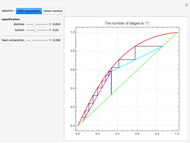
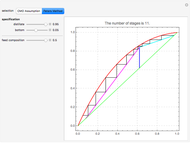
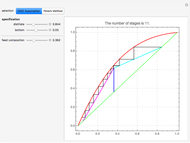
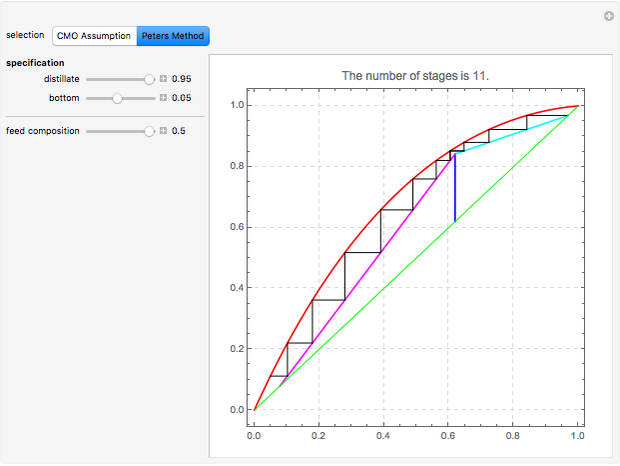
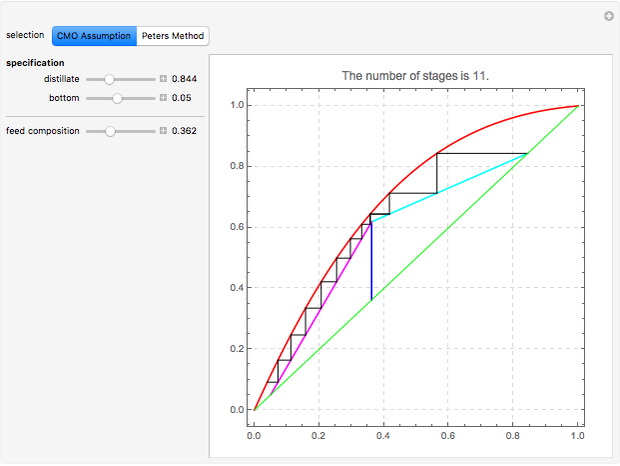
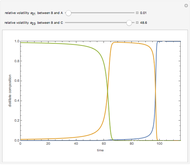
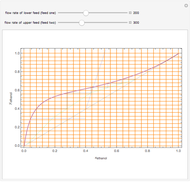
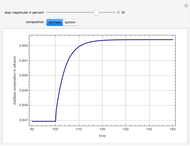
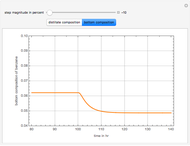
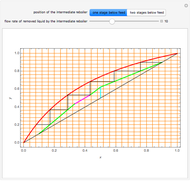
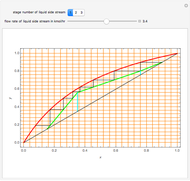
This Demonstration computes the number of theoretical stages needed to achieve a separation both with and without the CMO (constant molar overflow) assumption. It is observed, for this particular case, that the CMO analysis overestimates the number of theoretical plates. The binary mixture considered here is composed of ethanol and acetic acid. Vapor-liquid equilibrium data were obtained using a commercial process simulator (ASPEN Properties by ASPEN Technology Inc.) and the Wilson and the Hayden O'Connell models. The column is fed with saturated liquid. You can set the composition of the feed as well as distillate and bottom specifications. Since the two latent heats of vaporization of ethanol and acetic acid are quite different ( and
and  cal/g mol, respectively), one has to use a rigorous analysis where the operating curves are not linear. If the Peters transform is applied,
cal/g mol, respectively), one has to use a rigorous analysis where the operating curves are not linear. If the Peters transform is applied,
Contributed by: Housam Binous (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For more information, see:
M. F. Doherty and M. F. Malone, Conceptual Design of Distillation Systems, New York: McGraw–Hill, 2001.
J. R. Couper, W. R. Penney, J. R. Fair, and S. M. Walas, Chemical Process Equipment: Selection and Design, 2nd ed., Burlington: Gulf Professional Publishing, 2005.
Permanent Citation