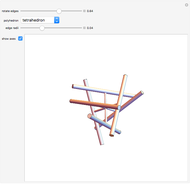
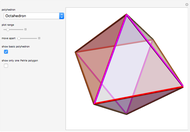
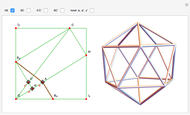
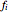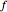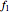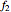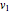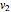Duals by Rotating the Edges of Polyhedra
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
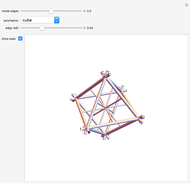
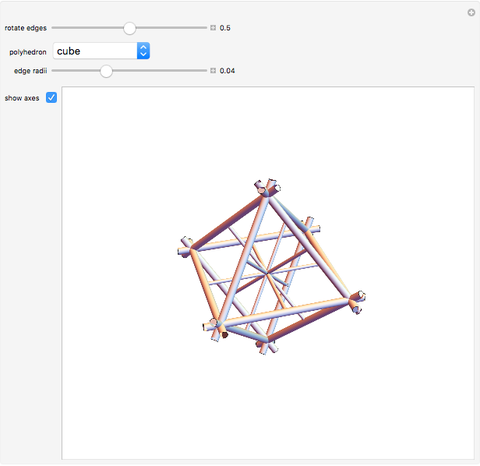
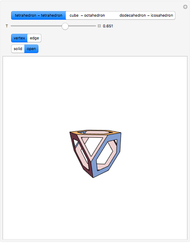
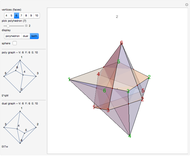
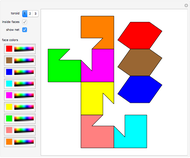
There are several ways to construct the dual  of a polyhedron
of a polyhedron 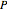 . Roughly speaking,
. Roughly speaking, 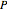 and
and  switch faces and vertices and the edges flip around. The dual of
switch faces and vertices and the edges flip around. The dual of  is
is 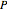 .
.
Contributed by: George Beck (March 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation