Dynamical Systems with Lorenz Attractors

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
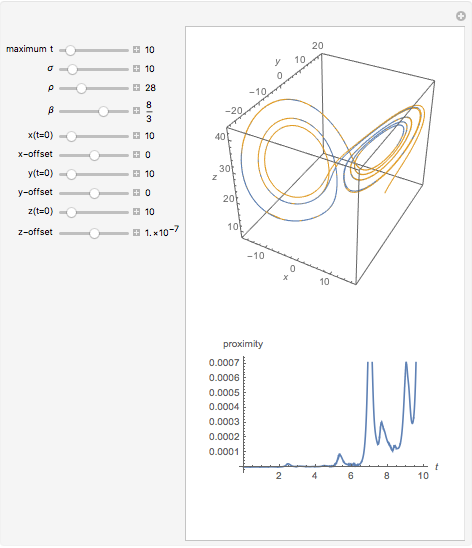
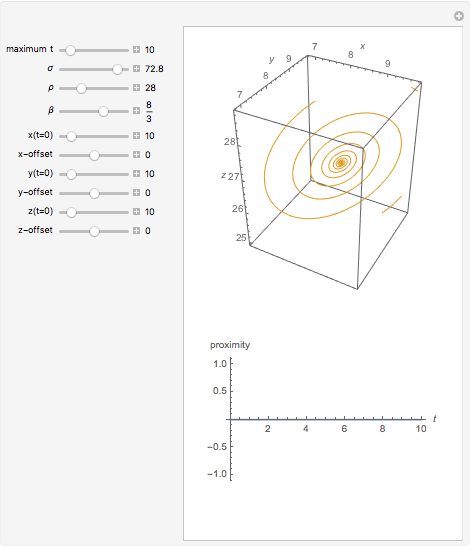
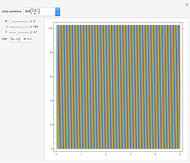
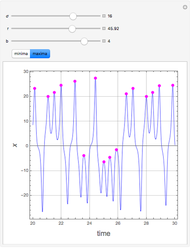
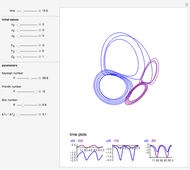
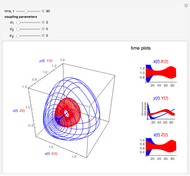
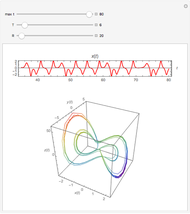
The Lorenz attractor is a nonlinear dynamic system that rose to fame in the early years of chaos theory. One of the most surprising features is its extraordinary sensitivity to initial conditions, a sensitivity that is not obvious when simply looking at the equations that define it. A minute fractional change in the initial conditions leads rapidly to a massive divergence in the path of the solution (popularized as "the butterfly effect"). The top graph shows two Lorenz attractors plotted with the same parameters except for the offset of the starting position. The bottom graph shows the length of the vector between the two solutions as a function of the curve parameter.
Contributed by: John Holland (June 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Lorenz attractor is defined by the system of equations
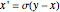 ,
,
 ,
,
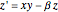 ,
,
where 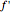 denotes the derivative of
denotes the derivative of 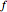 with respect to the parameter of the curve,
with respect to the parameter of the curve,  is the Prandtl number, and
is the Prandtl number, and  is the Rayleigh number.
is the Rayleigh number.
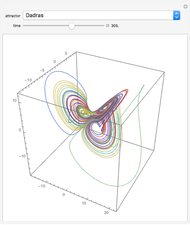
The Lorenz attractor shows how a very simple set of equations can produce astonishingly different results when given minutely different starting conditions. The weather is another example of such a system but has a much more complicated set of equations. Importantly, the Lorenz attractor shows that it is the nonlinear nature of the system rather than the inherent complexity of the defining equations that leads to the wildly unpredictable "chaotic" behavior.
This type of behavior was famously noticed in the first attempts at computerized weather modelling where the program output was a printout of the conditions at different points on a very simple model Earth at different times. When trying to rerun a portion of a simulation, Edward Lorenz copied the parameters from the start of the portion in question by hand back into the computer, but neglected to keep all of the decimal places that were available, instead rounding off to a lower precision. While initially the simulation ran in the same way, it quickly diverged from the path taken previously and soon became utterly different. This unpredictability still exists in weather forecasting today—even the tiniest change in the conditions at a single point on Earth, like the beating of a butterfly's wings, can lead to vastly different conditions everywhere else—this is the butterfly effect.
The growth in understanding of these types of systems spawned the whole field of chaos theory and has led to a better understanding of some of the most important unsolved problems in science today, for example, convection and turbulence, population dynamics, and disease control.
In fact, the set of problems that need chaos theory to be understood appears to be much larger than the set for which a solution without chaos theory exists.
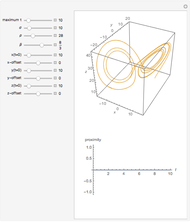
Snapshot 1: the Lorenz attractor with a minute offset (one part in 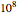 )
)
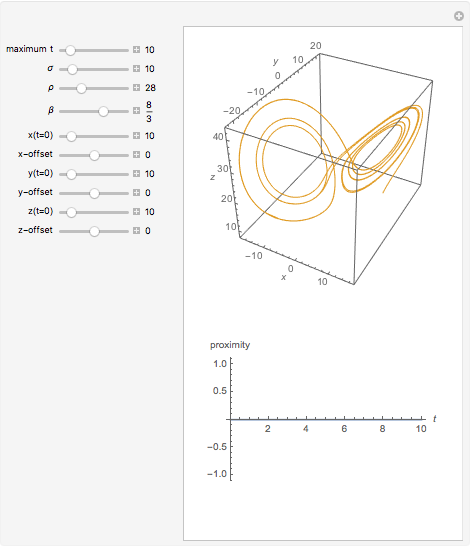
Snapshot 2: the same Lorenz attractor as in snapshot 1 but with no initial offset
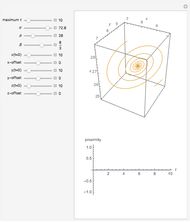
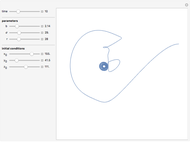
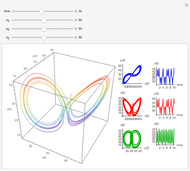
Snapshot 3: the Lorenz attractor with one loop and a minute offset (one part in 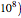
Snapshot 4: The same Lorenz attractor as in snapshot 3 but with no initial offset. With these parameters, notice that the divergence between the two attractors is of similar size to the fractional size of the initial offset with respect to the size of the whole attractor, a behavior that is more closely associated with human intuition about the linear systems we encounter every day.
Permanent Citation