Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Dynamics of a Charged Particle in a Magnetic Field with a Kicked Electric Field

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

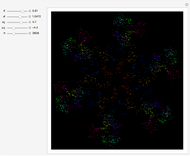
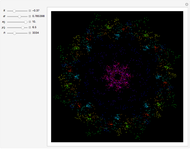
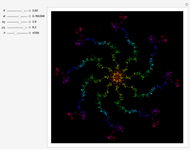
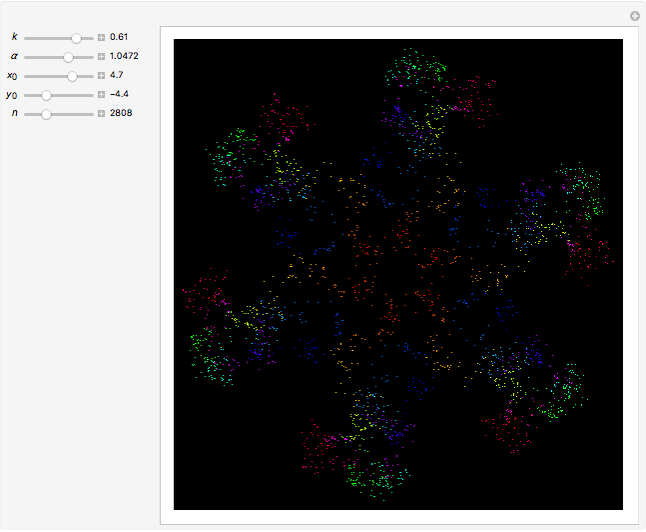
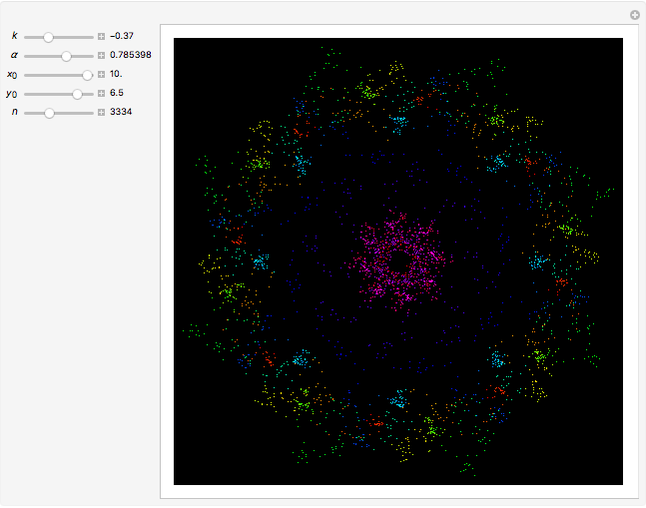
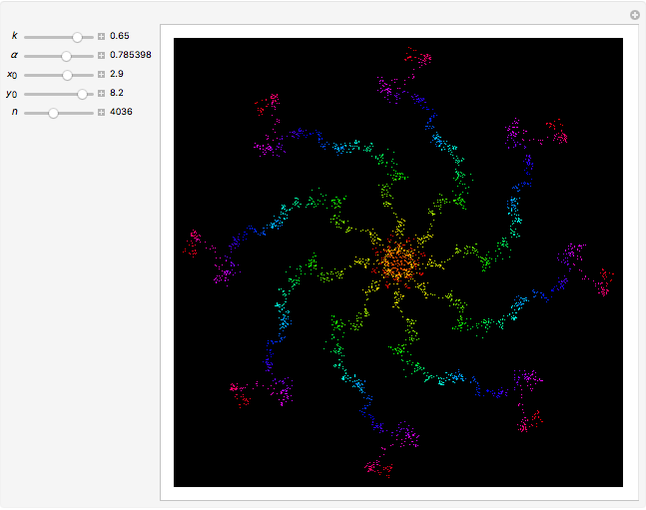
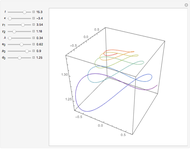
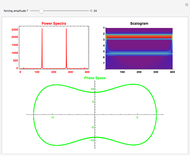
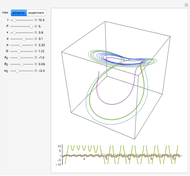
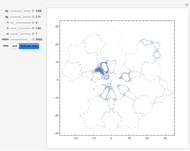
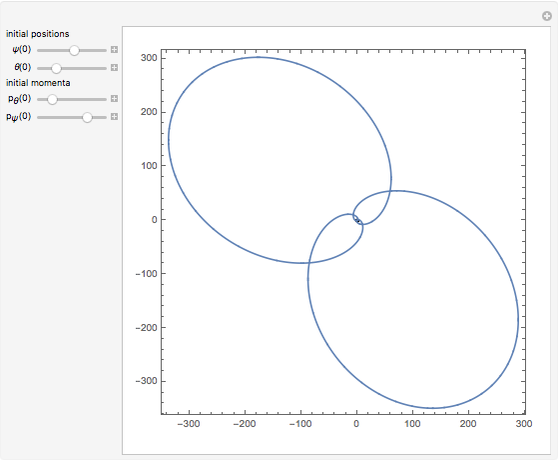
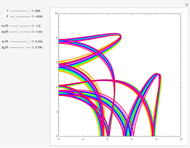
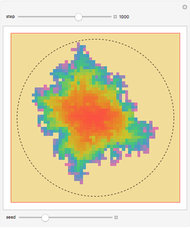
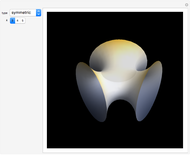
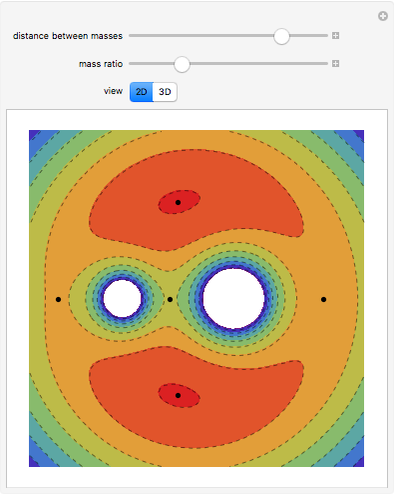
This web map is generated from the Hamiltonian for charged particles in an electric field in the presence of a constant uniform magnetic field with a periodically kicked linear oscillator. For , with integer values of , the kicks and oscillations enter into resonance and the particles diffuse, eventually covering the entire phase space. This is one classic example of chaotic dynamics.

Contributed by: Enrique Zeleny (August 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The map is determined by:

, ,

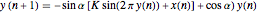where 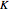is the intensity of the kicks and is the rotation angle between kicks.

References

[1] A. Lichtenberg and M. Lieberman, Regular and Chaotic Dynamics, 2nd ed., AMS 038, New York: Springer, 1992 p. 238.

[2] G. Zaslavsky. Scholarpedia, 2(10):3369 (2007). "Zaslavsky Web Map." (Aug 20, 2012) www.scholarpedia.org/article/Zaslavsky_web_map.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send