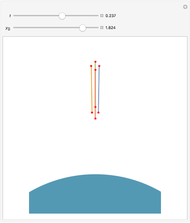
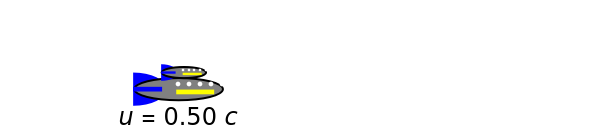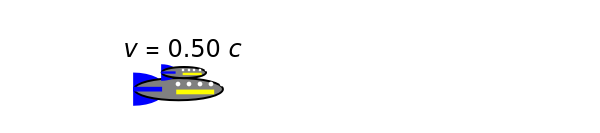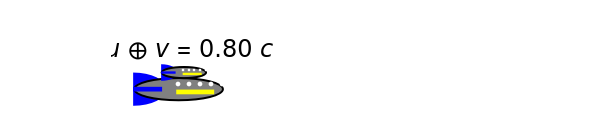Einstein's Formula for Adding Velocities

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
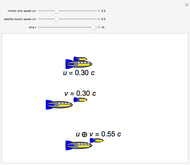
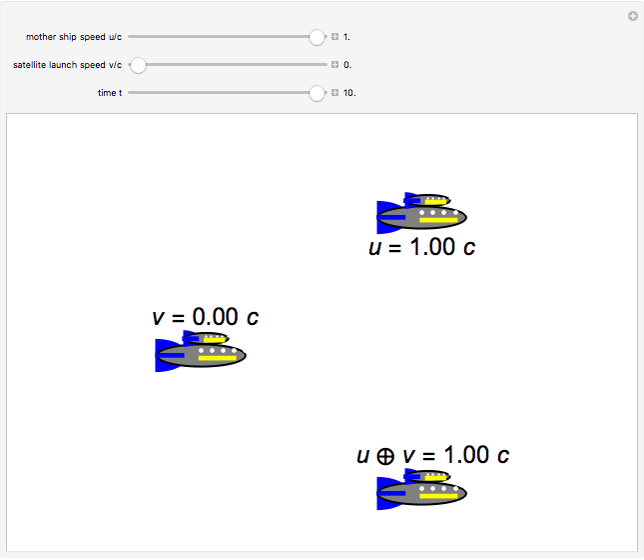
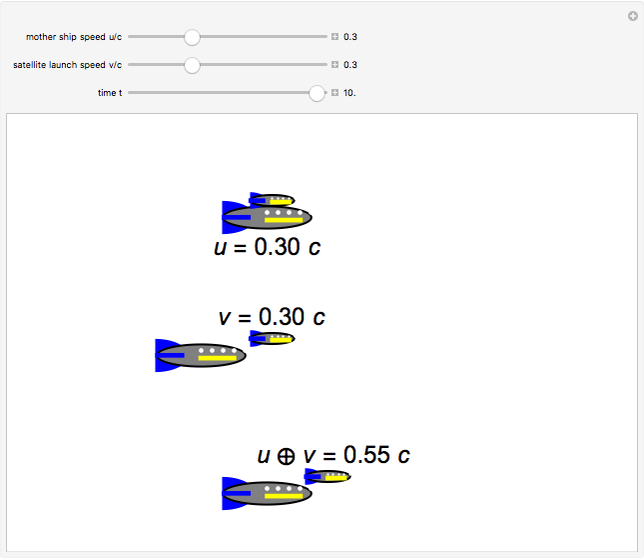
According to the special theory of relativity, the composition of two collinear velocities  and
and  is given by a well-known formula derived by Einstein:
is given by a well-known formula derived by Einstein: 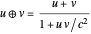 , where
, where  is the speed of light, 2.9979×
is the speed of light, 2.9979×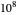 m/sec. For
m/sec. For 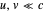 , this reduces to the simple Galilean formula
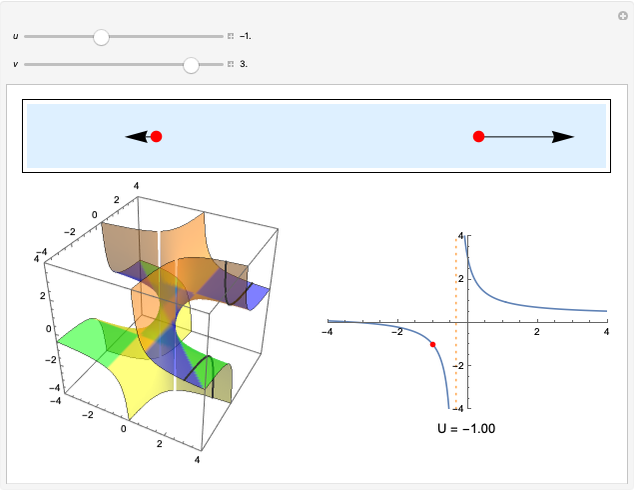
, this reduces to the simple Galilean formula  . The result can be derived by successive application of collinear Lorentz boosts, but it can be shown more intuitively by an argument outlined in the details. In the Demonstration the speeds are scaled as
. The result can be derived by successive application of collinear Lorentz boosts, but it can be shown more intuitively by an argument outlined in the details. In the Demonstration the speeds are scaled as  (also known as
(also known as 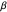 ) to keep the two rocket ships within the graphic. Einstein's formula is analogous to the law of addition for hyperbolic tangents,
) to keep the two rocket ships within the graphic. Einstein's formula is analogous to the law of addition for hyperbolic tangents,  , where
, where  corresponds to the rapidity, defined by
corresponds to the rapidity, defined by 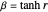 .
.
Contributed by: S. M. Blinder (April 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Suppose a baseball team is traveling on a train moving at 60 mph. The star fastball pitcher needs to tune up his arm for the next day’s game. Fortunately, one of the railroad cars is free, and its full length is available. If his 90 mph pitches are in the same direction the train is moving, the ball will actually be moving at 150 mph relative to the ground. The law of addition of velocities in the same direction is relatively straightforward, 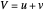 . But according to Einstein’s special theory of relativity, this is only approximately true and requires that
. But according to Einstein’s special theory of relativity, this is only approximately true and requires that  and
and  be small fractions of the speed of light,
be small fractions of the speed of light,  ≈ 3 ×
≈ 3 ×  m/sec (or 186,000 miles/sec). Expressed mathematically, we can write
m/sec (or 186,000 miles/sec). Expressed mathematically, we can write 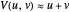 if
if 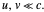 According to special relativity, the speed of light, when viewed from any frame of reference, has the same constant value
According to special relativity, the speed of light, when viewed from any frame of reference, has the same constant value  . Thus, if an atom moving at velocity
. Thus, if an atom moving at velocity  emits a light photon at velocity
emits a light photon at velocity  , the photon will still be observed to move at velocity
, the photon will still be observed to move at velocity  , not
, not 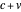 .
.
Our problem is to deduce the functional form of 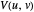 consistent with these facts. It is convenient to build in the known asymptotic behavior for
consistent with these facts. It is convenient to build in the known asymptotic behavior for  InlineMath by defining
InlineMath by defining  . When
. When 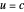 , we evidently have
, we evidently have 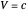 , so
, so 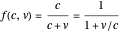 , and likewise
, and likewise 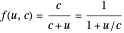 . If both
. If both  and
and  equal
equal  ,
, 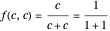 . A few moments' reflection should convince you that a function consistent with these properties is
. A few moments' reflection should convince you that a function consistent with these properties is 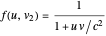 , which gives Einstein's velocity addition law
, which gives Einstein's velocity addition law 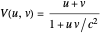 .
.
Reference:S. M. Blinder, Guide to Essential Math, Amsterdam: Elsevier, 2008 pp. 5–6.
Permanent Citation