Electron Waves in Bohr Atom

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
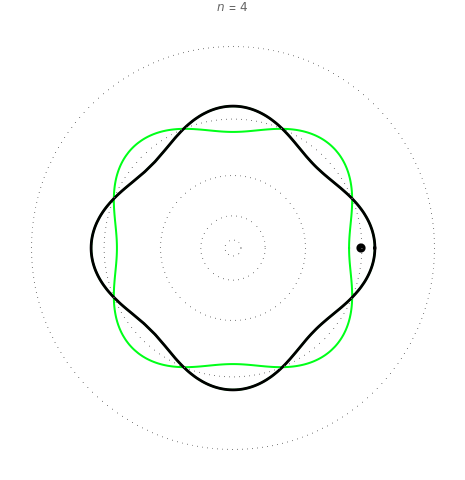
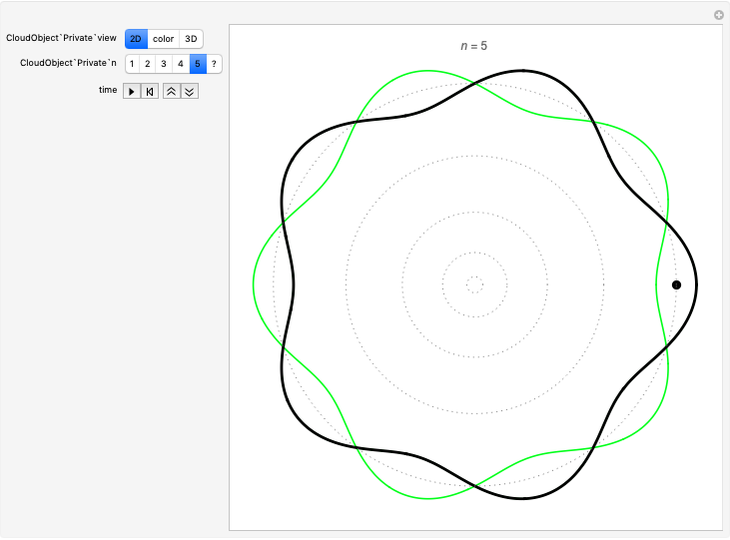
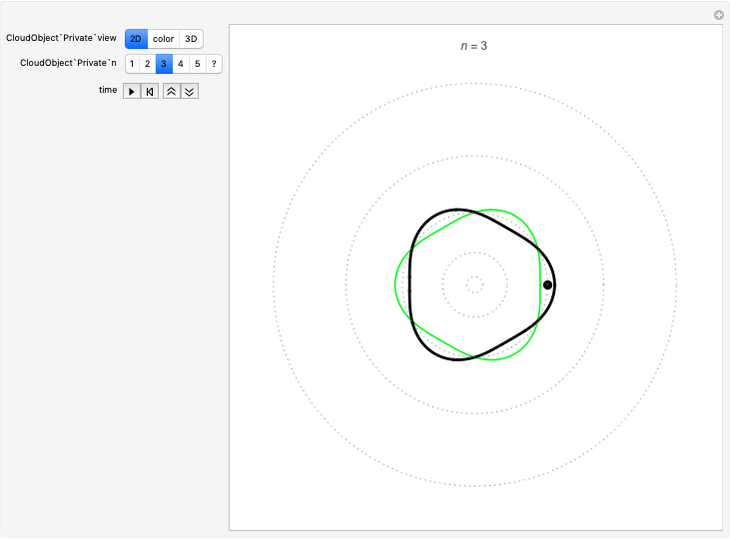
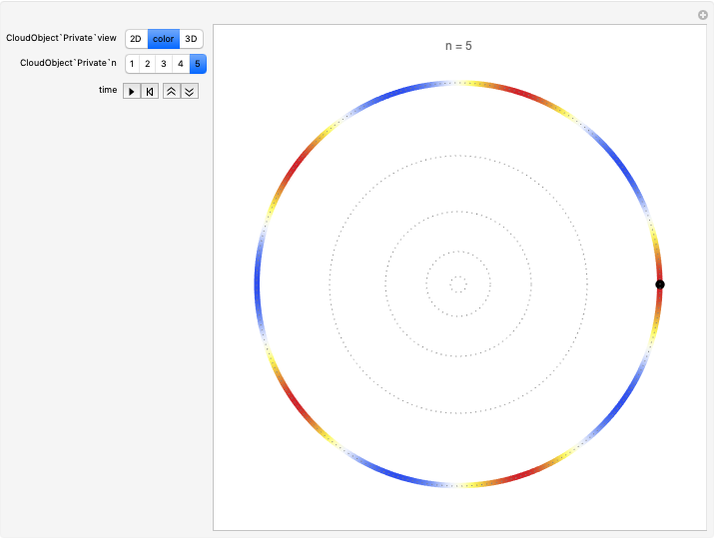
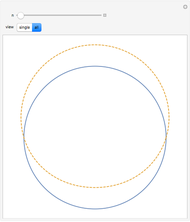
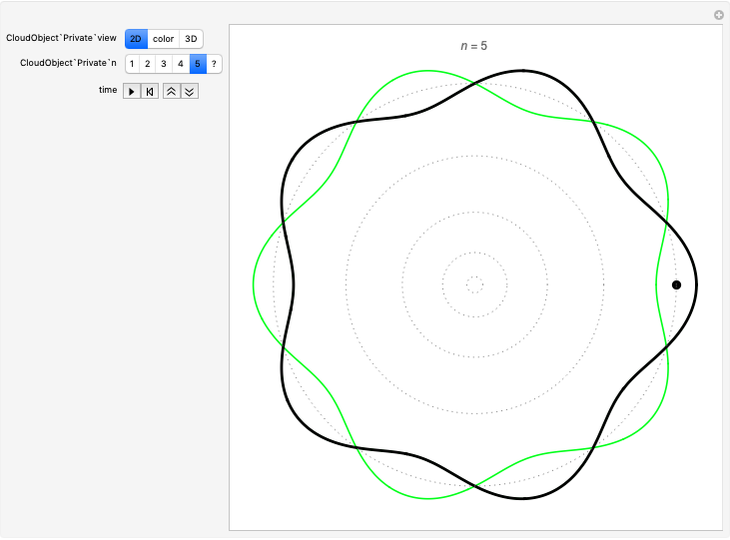
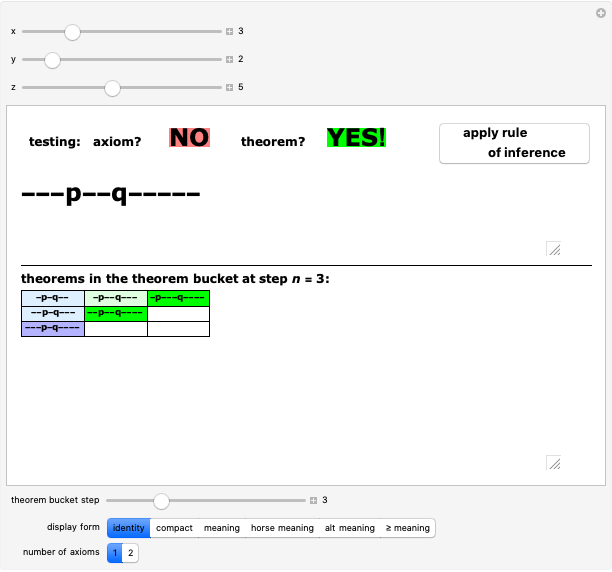
Quantization of orbits is an immediate consequence of treating the electron as a standing wave in the atom, with the principal quantum number 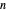 being the number of complete wavelengths that fit in one orbit. This Demonstration provides three different visualizations and buttons to select the quantum number, or (in "2D" view) a random decimal to show the destructive self-interference of the wave.
being the number of complete wavelengths that fit in one orbit. This Demonstration provides three different visualizations and buttons to select the quantum number, or (in "2D" view) a random decimal to show the destructive self-interference of the wave.
Contributed by: Kenneth E. Caviness (May 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Louis de Broglie's matter/wave-duality hypothesis suggested that any moving particle might be associated with a wave of wavelength 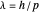 , where
, where  is Planck's constant and
is Planck's constant and 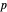 the momentum of the particle. Treating the electron in the hydrogen atom as a wave with periodic boundary conditions is equivalent to the quantization of angular momentum and so leads to the electron shells of Bohr's model, foreshadowing the full quantum-mechanical treatment based on the Schrödinger equation.
the momentum of the particle. Treating the electron in the hydrogen atom as a wave with periodic boundary conditions is equivalent to the quantization of angular momentum and so leads to the electron shells of Bohr's model, foreshadowing the full quantum-mechanical treatment based on the Schrödinger equation.
To emphasize that "what is waving" is irrelevant to the quantization effect, three quite different views of the wave are provided: 2D (in-out oscillation), color (with crests and troughs shown in red and blue), and 3D (up-down oscillation).
You can select small values of the positive integer quantum number 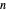 , and in the 2D view if you choose a random real number (using "?"), you get a wave that does not connect and begins to destructively interfere with itself, which is indicated by its fading away.
, and in the 2D view if you choose a random real number (using "?"), you get a wave that does not connect and begins to destructively interfere with itself, which is indicated by its fading away.
Click the appropriate buttons to run/pause, restart, speed up, or slow down the animation.
Permanent Citation