Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Motion of Pendulum with Varying Length

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

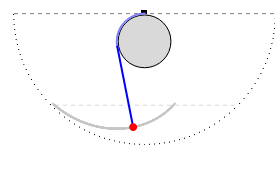
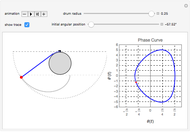
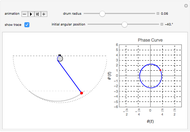
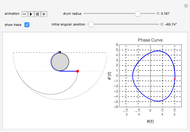
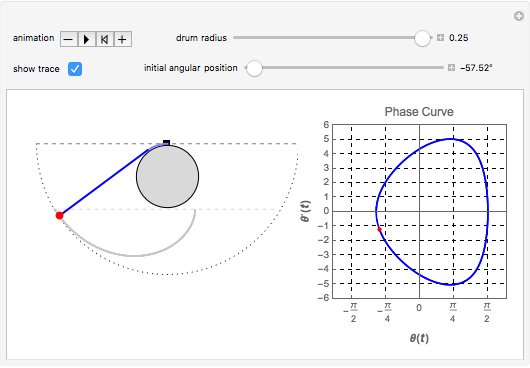
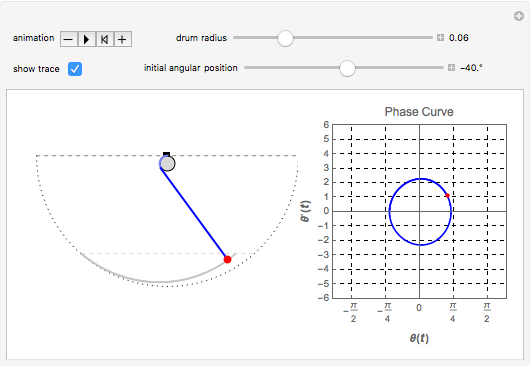
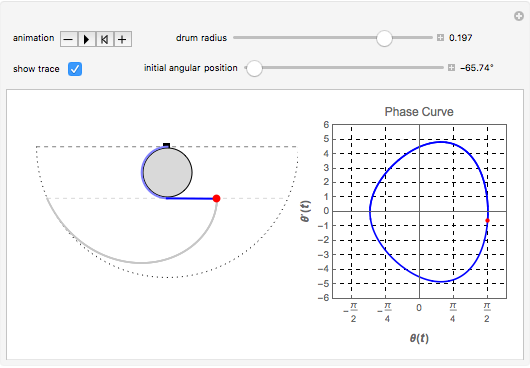
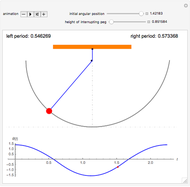
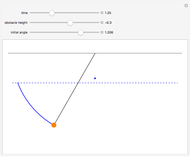
We consider a pendulum consisting of a bob hanging on a string attached to the top of a stationary cylindrical drum. When the pendulum is released from a position away from the vertical, it swings with a varying length, tracing a spiral-shaped path.

[more]

If the bob can swing to its maximum angle, it will reach its initial height (assuming there is no friction). This is a consequence of the conservation of energy.

[less]

Contributed by: Erik Mahieu (December 2012)
With additional contributions by: Franz Brandhuber
Open content licensed under CC BY-NC-SA

Snapshots

Details

Lagrangian mechanics can be used to solve this problem.

Let 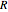be the radius of the drum, the length of the string, and 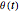the angle between the free part of the string and the vertical.

The potential energy is ,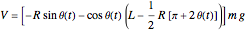

the kinetic energy is ,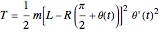

the Lagrangian is ,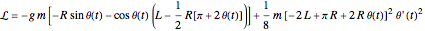

and the resulting equation of motion is .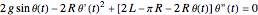

Since the string cannot support compression forces, the maximum initial angle has to satisfy the equation , keeping the bob under the lowest point of the drum.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send