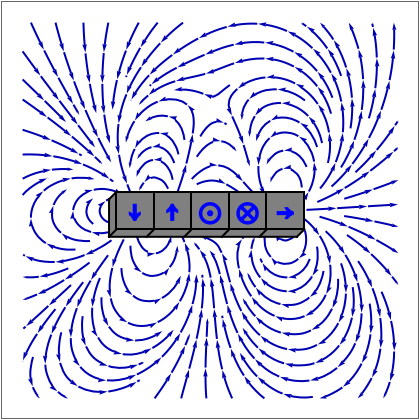
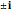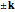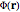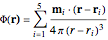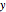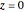Fields of Magnet Array

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
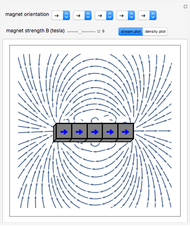
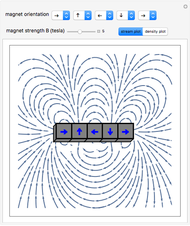
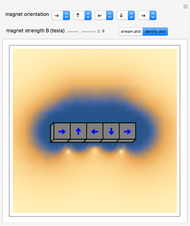
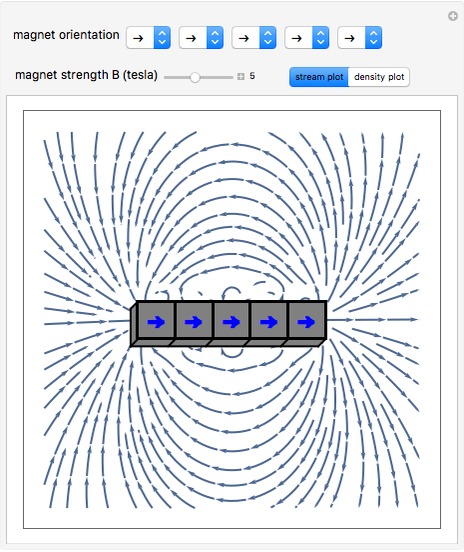
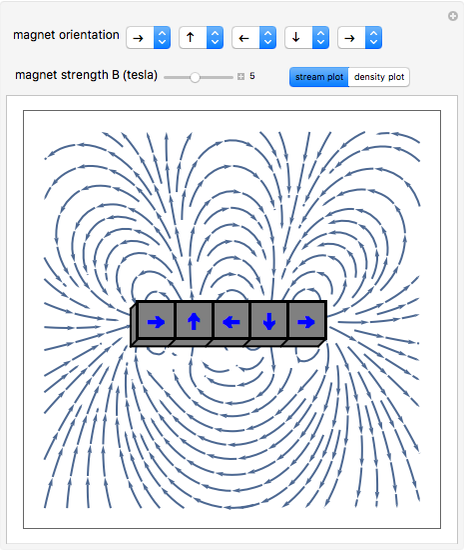
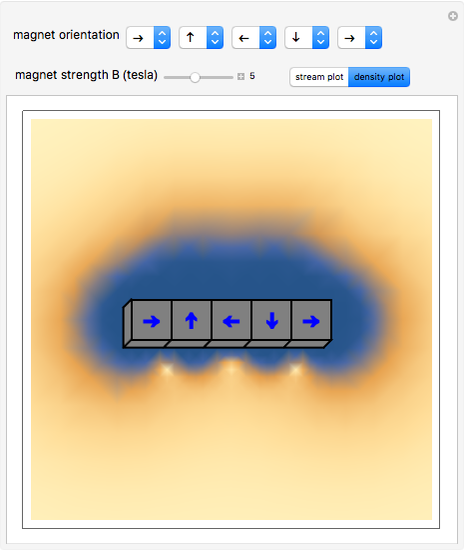
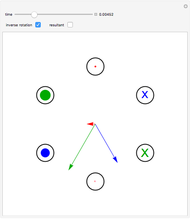
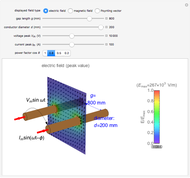
This Demonstration shows the magnetic fields produced by five 1 cm cubic magnets in a linear array. The magnets are held together by a copper axle (not shown), which keeps them from repelling one another but still allows each magnet to be rotated independently. (It is determined in advance which magnets can rotate with their dipoles parallel or normal to the axis.) The magnets have a field strength 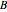 (more precisely, a magnetic remanence
(more precisely, a magnetic remanence 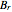 ) that can be selected between 1 and 10 T. Strong fields can be produces by "rare earth" magnets such as neodymium or samarium-cobalt. Since these are extremely brittle and subject to corrosion, they are nickel-plated.
) that can be selected between 1 and 10 T. Strong fields can be produces by "rare earth" magnets such as neodymium or samarium-cobalt. Since these are extremely brittle and subject to corrosion, they are nickel-plated.
Contributed by: S. M. Blinder (September 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: a simple bar magnet
Snapshot 2: Halbach array with large field on top side and much smaller field on bottom side
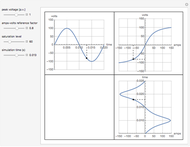
Snapshot 3: Halbach array field densities
Permanent Citation