Infinite Magic Elliptic Curves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
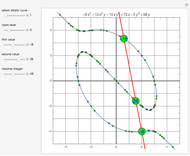
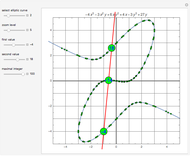
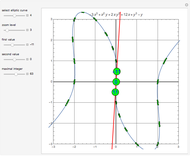
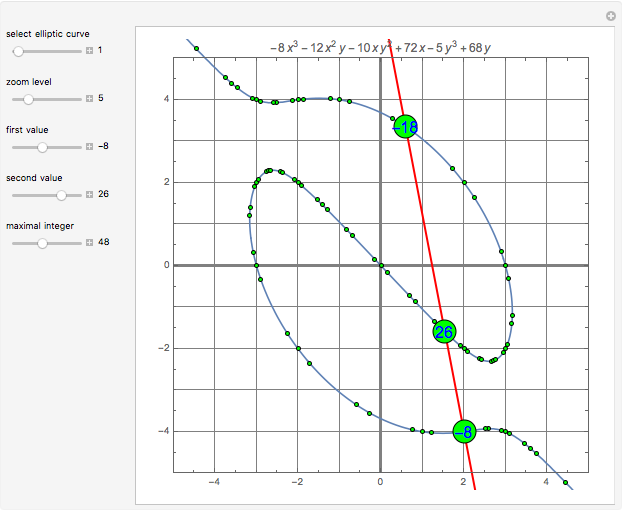
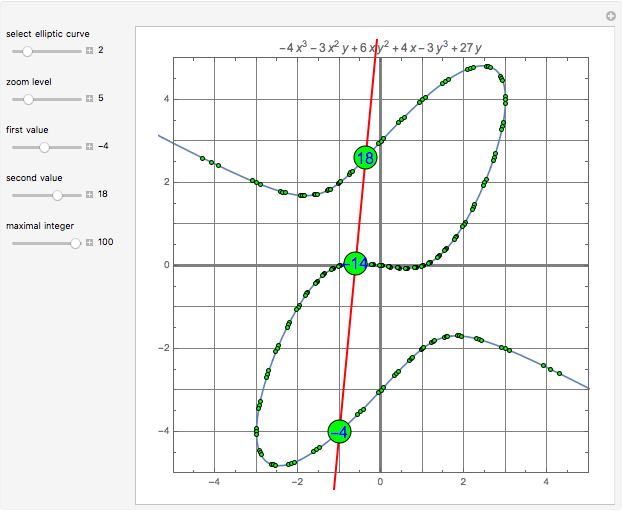
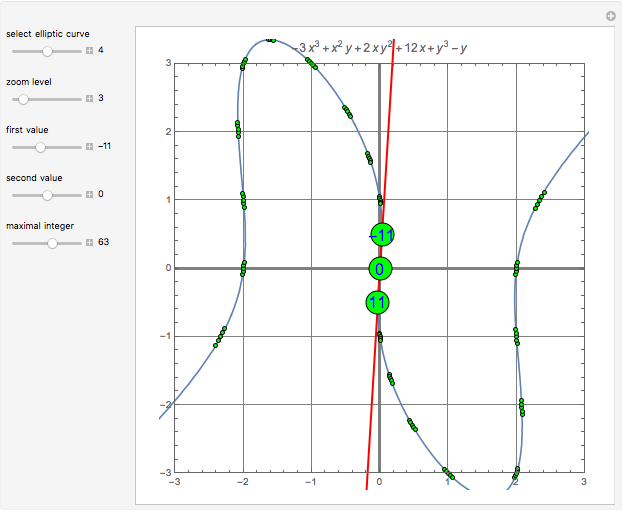
Can points representing integers be placed in the plane so that any triplet of integers summing to 0 lies on a straight line? It turns out the answer is yes. This Demonstration shows seven different ways to do it by placing the points on elliptic curves of the form 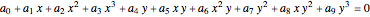 . Each of these curves can be warped in a variety of ways, but that does not change the ordering of the points on the curve.
. Each of these curves can be warped in a variety of ways, but that does not change the ordering of the points on the curve.
Contributed by: Ed Pegg Jr (December 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
There are various unsolved problems:
1. Are there other elliptic curves that give a different structure of integers?
2. Are there any asymmetrical elliptic curves that support a solution?
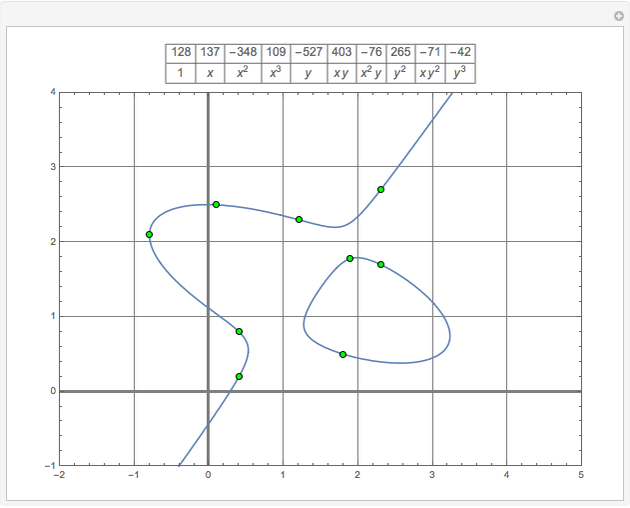
3. One way of finding the position of -42 on one of these curves is to find the intersection point of lines through the points 20, 22 and 19, 23. Is there a way that does not rely on line intersections?
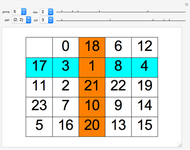
4. For the last curve, the first 40 points on one half of the curve are
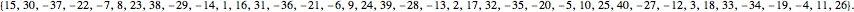
The integers are thus inserted at positions
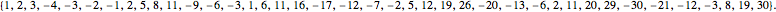
Is there an easy way to generate the infinite sequence?
Permanent Citation