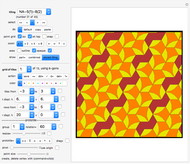
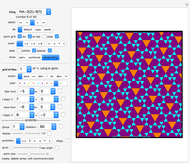
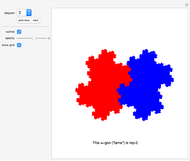
Neat Alternating Tilings of the Plane

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
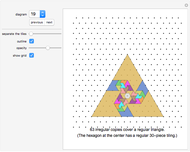
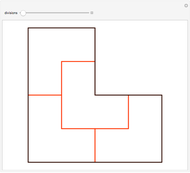
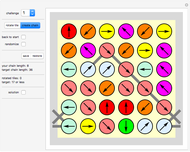
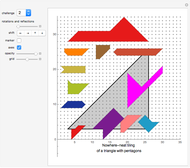
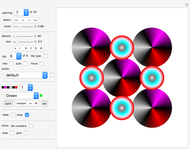
If adjacent tiles in a (polygonal) tiling always have a full side in common, the tiling is called neat.
[more]
Contributed by: Karl Scherer (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Introduction
Among all tilings for any given pair ( ,
,  ) we will try to find the ones with the least number of prototiles.
) we will try to find the ones with the least number of prototiles.
As a further investigation the reader might want to also find those solutions with a higher number of prototiles (some are displayed in Chapter 7 of the author's book New Mosaics).
In this Demonstration we will display at least one tiling for each ( ,
,  ) where
) where 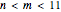 .
.
The following table gives you an overview of this chapter.
At the same time, it allows you to look up the number of prototiles that may give you a hint in case you want to find some tilings yourself.
Neat alternating tessellations of type ( ,
,  ) with a minimum number of prototiles:
) with a minimum number of prototiles:
(3,4) 3 (3,5) 3 (3,6) 2 (3,7) 3 (3,8) 3 (3,9) 2 (3,10) 3 (4,5) 3 (4,6) 2 (4,7) 2 (4,8) 2 (4,9) 2 (4,10) 2 (5,6) 3 (5,7) 4 (5,8) 3 (5,9) 3 (5,10) 2 (6,7) 3 (6,8) 3 (6,9) 2 (6,10) 3 (6,12) 2 (7,8) 3 (7,9) 3 (7,10) 3 (8,9) 3 (8,10) 3 (9,10) 3 (9,11) 3
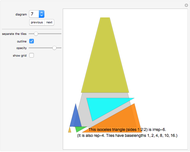
For example, the entry "(3,5) 3" means that a neat alternating tiling needs at least three prototiles, that is, it either is constructed from two triangular prototiles and one pentagonal prototile or from one triangular prototile and two pentagonal prototiles. Of course, it is of interest whether a solution exists for both cases.
These cases are reflected in the names of the tilings: a solution to the first case is called NA-3(2)-5(1), and a solution to the second case is called NA-3(1)-5(2).
Mathematical Theorems
Here are some upper bounds for the minimum number of prototiles for neat alternating tilings of the plane.
Let  and
and  be natural numbers such that
be natural numbers such that 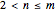 .
Then there exists a neat alternating inclusion-free tiling
.
Then there exists a neat alternating inclusion-free tiling 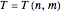 of the plane using
of the plane using  -sided and
-sided and  -sided polygons.
Furthermore, the number of its prototiles is not greater than
-sided polygons.
Furthermore, the number of its prototiles is not greater than
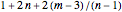 and also, independent of
and also, independent of  , not greater than
, not greater than
 .
Hence in general we can state that
.
Hence in general we can state that
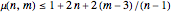 and also, independent of
and also, independent of  , that
, that
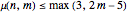 .
Here "inclusion-free" means that no tile totally surrounds any other tile.
.
Here "inclusion-free" means that no tile totally surrounds any other tile.
New Findings
The solution NA-3(1)-10(2) shown in this Demonstration is new. It is the first of its type ever published.
The tiling NA-5(1)-8(2) presented in this Demonstration is new and published here for the first time.
All other tilings are taken from the book New Mosaics by the same author, see Reference below.
Unsolved Problems
Find a tiling of type NA-5(2)-6(1) or prove that there is none.
Find a tiling of type NA-5(2)-7(1) or NA-5(1)-7(2) or prove that there is none.
Can you find a tiling of type NA-5(2)-8(1) or prove that there is none?
Reference
The first half of the book New Mosaics, privately published 1997 by the same author, investigates the topic of neat alternating tilings in detail.
Controls
The controls in this Demonstration are identical to the ones in the Demonstrations "Nowhere-Neat Tilings of the Plane" and "Nowhere-Neat Tilings of the Plane, Part 2", so you might be already familiar with them. Click "show, part+" to start editing a part.
Control: "select"
The options "<<", "<", ">", and ">>" select the first, previous, next, and last stored tiling, respectively.
Control: "do"
Reset: Click "default" to restore the current tiling to its default. All editing information of this tiling will be lost.
Copy: Click "copy" to mark the current tiling. It will be used later by the "paste" option.
Paste: Click "paste" to paste the marked tiling to the current position, thereby replacing the current tiling.
Control: "point grid"
The "point grid" control contains four on/off buttons:
• The first button makes the integral lattice grid visible/invisible.
• The second button toggles between the ortho(gonal) grid and the iso(metric) grid. Note that changing the grid type can distort an existing tiling since the tiling data is based on counting grid increments: the unit of height in the orthogonal grid is 1, but in the isometric grid it is 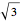 . That is why the ortho/iso selection is always stored together with the tilings.
. That is why the ortho/iso selection is always stored together with the tilings.
• The third button controls whether the grid is placed on top of or underneath the tiling.
• The fourth button controls whether the currently edited vertex should snap to the grid. The "snap" setting is stored with the tilings.
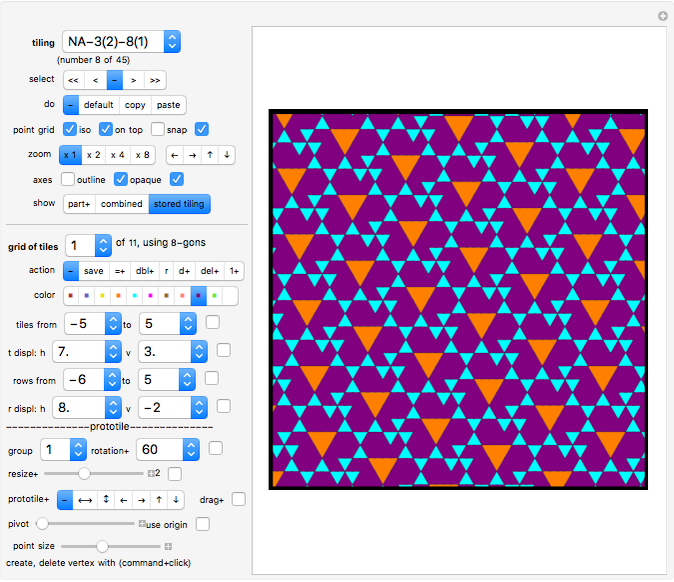
Control: "grid of tiles"
The tilings are constructed as a union of "tile grids". For each tile grid, a prototile is specified and that is then copied to a grid of positions. All copies will carry the same color. In the given examples the grids never overlap. See below to find out how the grid of positions is specified.
The system stores the grid specifications rather than the data for each tile. Hence for each display the system re-creates the tiling from the stored sets of its prototiles and the associated grid specifications.
Control: "zoom"
This control comes in handy when you create and edit the prototile of the current grid of tiles. When you have zoomed in, you can shift the zoom window with the four arrow buttons next to the zoom options.
Control: "show"
Clicking the option "part+" will display only the selected grid of tiles (or—if group is greater than 0—the selected group of tile grids, starting with the current one). The current tile grid can then be edited. Click the "save" button in the "action" setter bar to store the edited tile grid.
Clicking the option "combined" will enter the edit mode and display the stored tiling with the edited grid of tiles (combining the new part with the old parts). The old grid of tiles with the same number will not be shown. Click the "save" button in the "action" setter bar to store the edited tile grid.
Clicking the option "stored tiling" will display the stored tiling, ignoring the editing of the current tile grid. While "stored tiling" is selected the edit mode is switched off; hence you cannot use any of the "action" options.
If the show option "stored tiling" is active, selecting a new tile grid (or changing any other tile grid settings) will automatically switch to the option "combined" and start the edit mode.
Control: "action"
Store: Click "save" to store your edited tile grid.
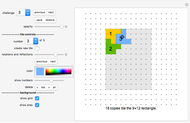
Double range: Click "dbl+" to create a copy of the current tile grid or a group of tile grids. The current grid will be saved first. The new grid(s) will be inserted at the next position(s) after the old group of tile grids. All the following entries will be renumbered. The system will update the tile grid number to display the number of the new tile grid. The new "current" grid will be the first grid of the newly copied set.
Reset: Click "r" to reset the specifications of the currently selected tile grid to the last stored values ("color", "tiles from...to", "t displ", "rows from...to", "r displ").
Default range: Click "d+" to reset to default the specifications of the current grid and the next grids, the total number being given by the "group" selection. All editing information of these tile grids will be lost.
Delete range: Clicking "del+" will delete the current tile grid and also a few other tile grids with higher numbers (the number of elements in this group is given by the "group" drop-down menu). For technical reasons the last grid of a tiling cannot be deleted, hence "del+" does not work if all tile grids would be deleted.
Shuffle tile grids: Clicking option "1+" will shift a group of tile grids, beginning with the current one, to the start of the queue. This is a simple tool to shuffle the tile grids. The number of tile grids in the group is given by the "group" selection.
Color selection
Clicking a color starts the edit mode (if it is not yet active).
For purely aesthetic reasons, the colors in the given tilings have been chosen so that no two adjacent tiles carry the same color. Of course having adjacent tiles always of different colors often means that more grids are necessary for the definition of the tiling.
For the condition of the tiling being nowhere-neat the choice of colors is irrelevant.
Controls: specification of grid positions
Clicking a specification of grid positions will start the edit mode (if it is not yet active).
A grid of positions (for the copies of the given prototile) is specified as follows:
The tile displacements ("t displ") show how far the next tile is from the previous tile in the same row of tiles ("h": horizontal displacement; "v": vertical displacement).
The "from" and "to" entries define where the row starts and ends. (If a row extends beyond the screen frame, it usually means that it should go on forever.)
The row displacements ("r displ") show the displacement between one row and the next. Again, the "from" and "to" entries define how many rows there are to be displayed.
Note that the prototile itself and the row containing the prototile have the number 0, since the entries "from" and "to" define the number of steps between the start and end of the row!
Some tilings contain "tile grids" that consist only of one tile, a few tiles, or a single row of tiles.
After each position control there is a checkbox. Clicking it (in edit mode) will set the two associated controls to zero (after putting them in temporary storage). If you click it when both controls are zero, then the values will be restored from temporary storage.
Changing any tile grid parameter automatically invokes the edit mode (if it is not active already).
Editing the prototile
Start the edit mode (for example, by selecting the "show" control "part+" or "combined"). You will see a polygon whose vertices are marked by large dots. This is the "prototile" of your tile grid.
The prototile determines what all the tiles in the grid will look like. Click the "color" setter bar to change the color of the prototile. Move the vertices to change the shape of the prototile. If you have this selected, the vertices of your prototile will snap to the selected grid.
You can add a vertex with Alt-click in Windows or Option-click in Mac OS.
After moving the cursor to a marked vertex, you can delete a vertex (again with Alt-click or Option-click).
Control: "group"
Here you decide how large a group of tile grids that you want to manipulate simultaneously. The group of tile grids begins with the current one.
All controls that carry a plus sign "+" are able to affect a whole group of tile grids at once. These are: show part ("part+"), save from-to parameters ("=+"), double ("dbl+"), default ("d+"), delete ("del+"), move to first in row ("1+"), all shift and mirror controls for prototiles (" ", "
", " ", "
", " ", "
", " ", "
", " ", "
", " "), rotation ("rotation+"), and drag ("drag+"). Note that the reset option (button "r" in the "action" setter bar) only applies to the current tiling grid, but not for groups of tiling grids.
"), rotation ("rotation+"), and drag ("drag+"). Note that the reset option (button "r" in the "action" setter bar) only applies to the current tiling grid, but not for groups of tiling grids.
Control: rotate prototile or prototile group
Select a rotation from the drop-down menu, then activate it by clicking the checkbox next to it. You can click the checkbox several times in a row (but give the system time to react in between).
If "group" > 1 is selected, any rotation will affect a group of tile grids, beginning with the current one. This way you can rotate groups of prototiles around the same point. (Note that this does not rotate the resulting tiling!) All changes will be immediately saved, so you do not have to click the "save" button afterward.
If "pivot" > 0 is selected, the rotation will be around the selected vertex; otherwise the group will rotate around the center of the group. If "use origin" is selected, the origin is used as the fixed point for the rotation.
Control: resize prototile or prototile group
Set the "resize+" slider to the desired value and then click the checkbox next to it. The current tile will be enlarged by the amount given by the "resize+" slider. If "pivot" > 0 is selected, the fixed point of the resizing will be the selected vertex; otherwise the fixed point will be the center of the prototile.
If "group" > 0 is selected, resizing will affect a group of tile grids, beginning with the current one. All changes will be immediately saved, so you do not have to click the "save" button afterward.
If "pivot" > 0 is selected, the fixed point of the resizing will be the selected vertex; otherwise the fixed point will be the center of the prototile. If "use origin" is selected, the origin is used as the fixed point for resizing.
Control: process prototile or prototile group
The options of the setter bar allow you flip the prototile horizontally (" ") or vertically ("
") or vertically (" ") or shift it in one of four directions ("
") or shift it in one of four directions (" ", "
", " ", "
", " ", "
", " ").
").
If "group" > 1 is selected, the shift and mirror operations will affect a group of tile grids, beginning with the current one. All changes will be immediately saved, so you do not have to click the "save" button afterward.
If "pivot" > 0 is selected, the fixed point of the mirroring will be the selected vertex; otherwise the fixed point will be the center of the group of prototiles. If "use origin" is selected, the axes are used for mirroring.
Control: drag prototile or prototile group
Clicking the "drag+" button starts a drag mode, which then stays active until the button is clicked again. In drag mode the whole prototile moves anywhere you want it. Just click the target position or drag a vertex. If "pivot" = 0, the closest vertex will be moved to the designated position. Otherwise the selected vertex will be moved to the designated position.
If "group" > 1 is selected, the drag operation will affect a group of tile grids, beginning with the current one. All changes will be immediately saved, so you do not have to click the "save" button afterward.
Control: "pivot"
Here you can select a pivot (a handle) for your rotation, flip, and drag operations. Moving the slider will cause one of the prototile's vertices to turn gray. This vertex will then be used by the rotate, flip, and drag processes mentioned above.
If "pivot" = 0 (which is the default), then the axes and their intersection point will be used for the rotate and flip processes. If "use origin" is selected, the origin is used as the fixed point for the rotations and mirroring.
Note
If many polygons are displayed, the system can be slow to react to your input. If a click does not have an effect, click another button first (click a neutral "-" button), then go back to your previous click. Give the system time to react!
Permanent Citation