Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Mona Lisa and the Golden Rectangle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

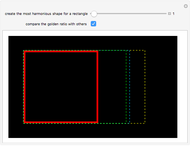
The ancient Greeks thought that the most pleasing proportions for a rectangle were those in which the rectangle's sides were in the ratio of about 1.618 to 1. This number is called the golden section or golden ratio and a rectangle with those proportions is called a golden rectangle.

[more]

Leonardo da Vinci referred to the golden ratio as the "divine proportion". There are several features of his most famous painting, the Mona Lisa, to which a golden rectangle can be fitted. See how many of these you can find by varying the orientation, position, and size of the rectangle.

[less]

Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA

Details

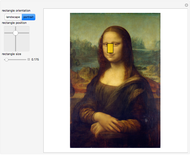
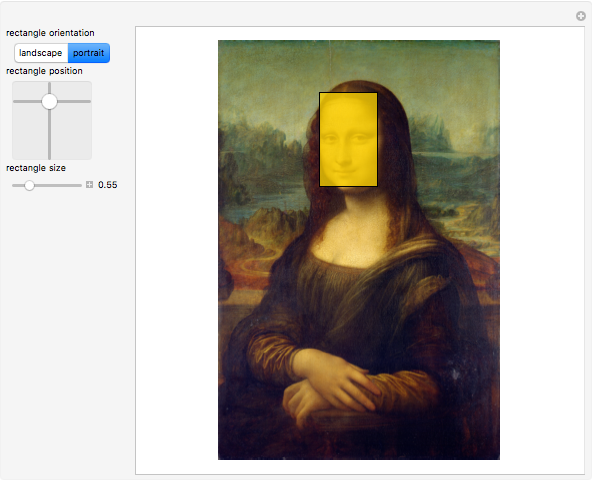
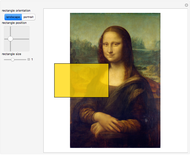
Snapshot 1: Mona Lisa's face can be neatly enclosed by a golden rectangle

Snapshot 2: so can her Roman nose; you can also fit smaller horizontal rectangles to her eyes and mouth

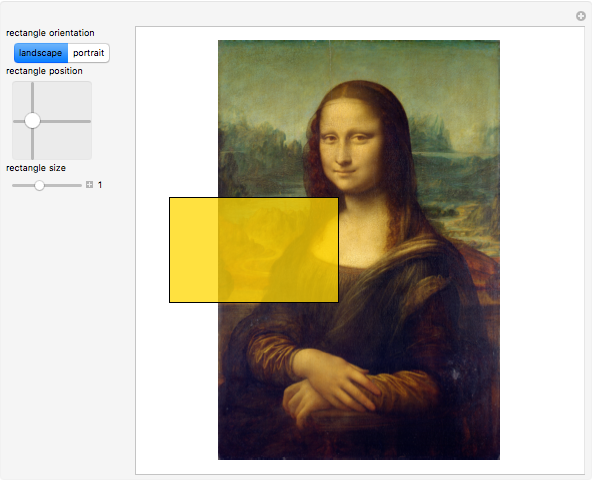
Snapshot 3: finally, the frame of the entire painting is near the divine proportion

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send