Line Art

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
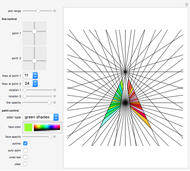
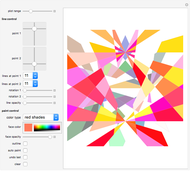
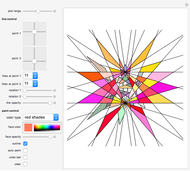
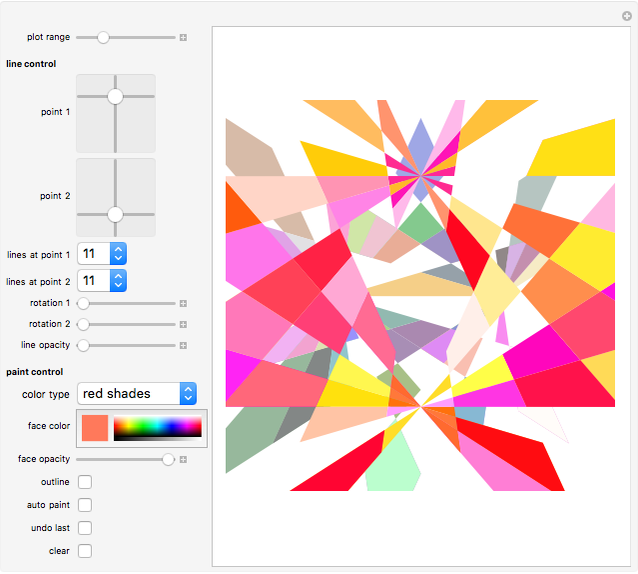
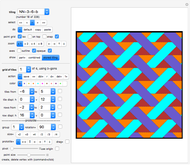
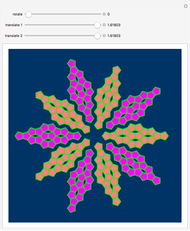
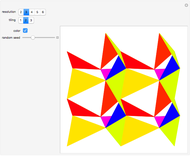
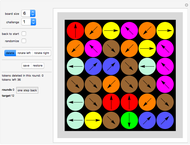
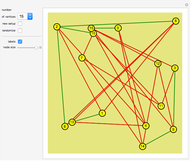
This Demonstration allows you to (manually or automatically) create very decorative artwork purely based on the coloring of areas created by intersecting lines.
Contributed by: Karl Scherer (March 2011)
Additional contributions by: Dennis Van Straten
Open content licensed under CC BY-NC-SA
Snapshots
Details
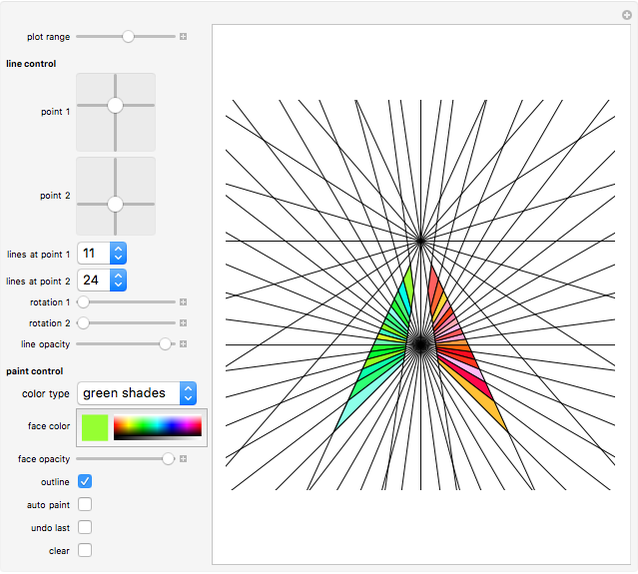
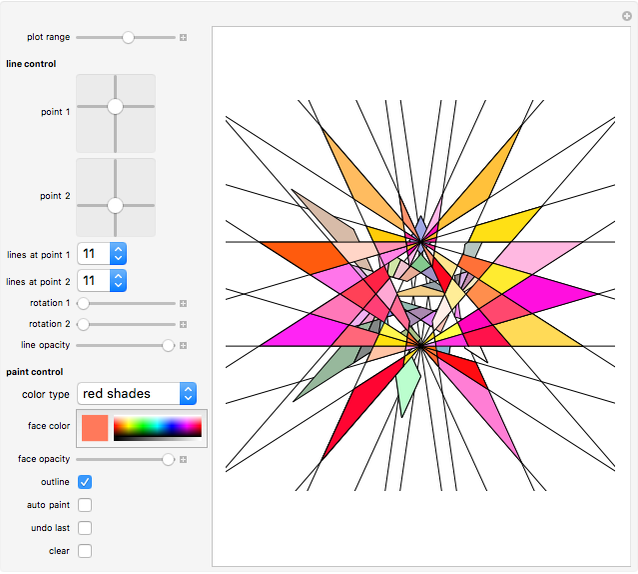
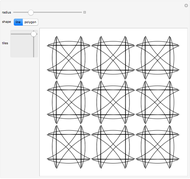
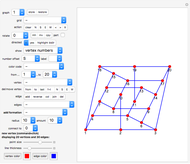
You are presented with two bundles of lines converging at positions "point 1" and "point 2".
You can color an area simply by clicking the board.
The "plot range" slider allows you to zoom in and out.
Line Control:
Use the 2D controls to specify the positions of the two points where the lines meet.
You can also select how many lines converge at each point.
Sliders "rotation 1" and "rotation 2" allow you to rotate the line bundles around their pivots.
Use the "line opacity" slider to make the lines less visible or invisible.
Paint Control:
Click the board to paint a selected area. If the area is too large (i.e., larger than the plot range), it will not be colored.
Use the "color type" drop-down menu to select color schemes for your manual or automatic painting.
Use the "face color" gradient to set the color you want.
Use the "face opacity" slider to make the colored areas more or less transparent.
Click "outline" to switch polygon outlining on or off.
Option "auto paint" allows the system to automatically paint randomly selected areas. This is the fastest way to create a painting.
Click "undo last" to undo the last painting step.
Finally, the "clear" button deletes all historic painting information and shows a white board.
Recommendation:
Some special effects arise from changing the 2D controls, the number of converging lines, and the color type several times during the painting process. Explore!
Math:
The areas colored are defined by pairs of lines crossing each other, hence these areas are quadrilaterals, which are either convex or X-shaped (hourglass figure). If an area is too large (some areas go to infinity), it will not be colored.
History:
This Demonstration is based on an idea by the author's friend Dennis Van Straten.
Permanent Citation
"Line Art"
http://demonstrations.wolfram.com/LineArt/
Wolfram Demonstrations Project
Published: March 7 2011