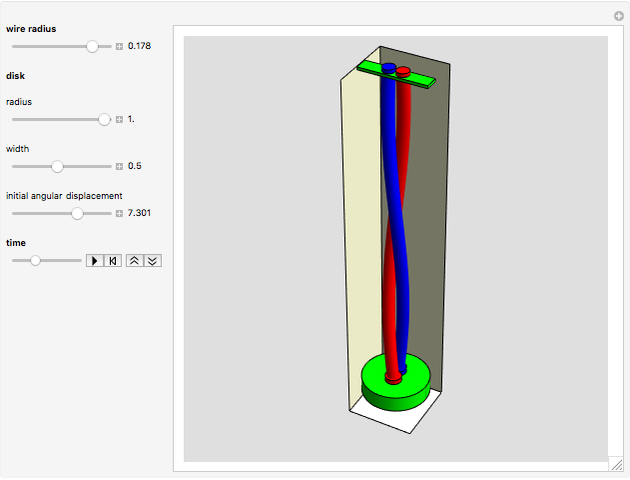
Torsional Pendulum Suspended by Two Stranded Wires

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
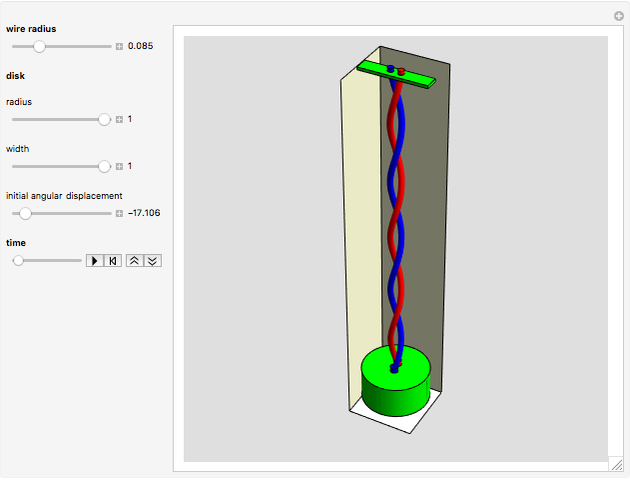
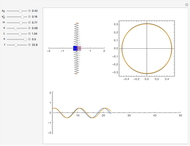
This Demonstration simulates a variation of the classic torsional pendulum.
[more]
Contributed by: Erik Mahieu (February 2017)
Open content licensed under CC BY-NC-SA
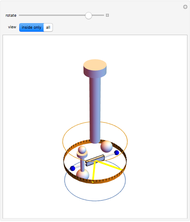
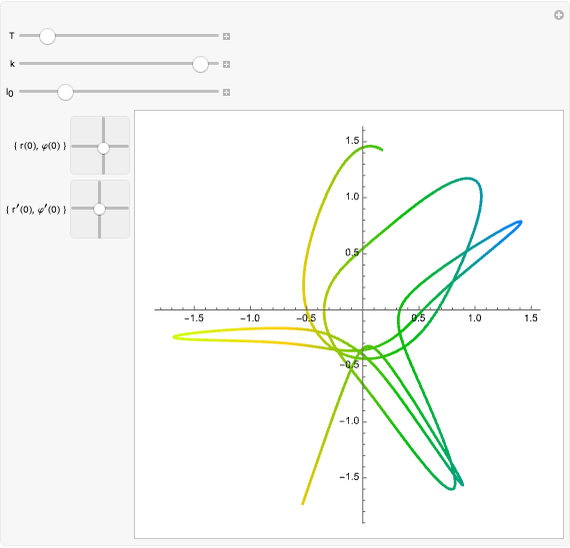
Snapshots
Details
This system has one degree of freedom, 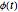 , the angular displacement of the suspended disk at time
, the angular displacement of the suspended disk at time  .
.
The potential energy of the system is 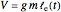 .
.
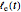 is the effective length of the strand after twisting by the angle
is the effective length of the strand after twisting by the angle  :
: 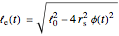 , where
, where
 is the length of the untwisted strand, and
is the length of the untwisted strand, and
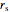 is the radius of the strand or
is the radius of the strand or 
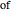 the distance between the
the distance between the 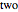 wires.
wires.
The kinetic energy of the system is 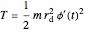 , where
, where
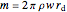 is the mass of the disk,
is the mass of the disk,
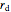 is the radius of the disk,
is the radius of the disk,
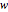 is the width of the disk, and
is the width of the disk, and
 is its density.
is its density.
The Lagrangian of this system is  .
.
Substituting this in the Euler–Lagrange equations for 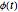 gives:
gives:
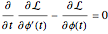 ,
,
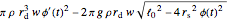 .
.
This results in the equation of motion:
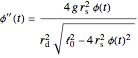 .
.
Permanent Citation