Details

Before exploring this system, you should investigate the MIU-system, the pq-system and the tq-system (see links below). You should already know the meaning of the "C-type" theorems in the tq-system and have considered the question of what C-type statements are not theorems of the system.

Exploring the System

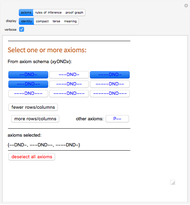
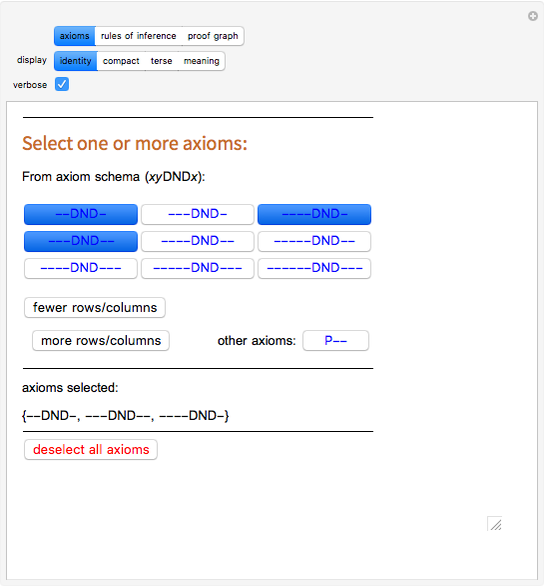
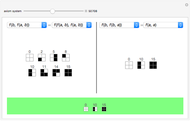
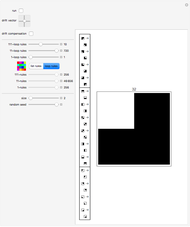
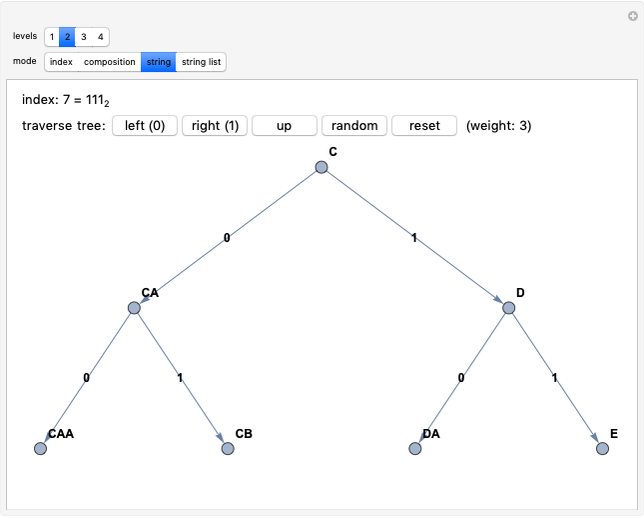
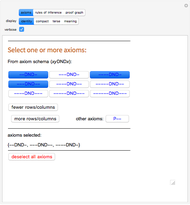
Snapshot 1: the axioms page with three axioms selected: the axioms needed to prove "P-----" ("P5" in compact display form)

First select the axioms you want to use, by clicking buttons on the "axioms" page. The buttons toggle which axioms will be used to generate theorems. Shown on this page are a sample of axioms matching the axiom schema, a list of the axioms you have selected, buttons to show more or fewer rows and columns, a button to toggle the use of the "extra" axiom, and a button to deselect all axioms. There is an infinite number of axioms to choose from, but to begin with, click the first button to select the axiom "--DND-" (which in "compact" display form is "2DND1").

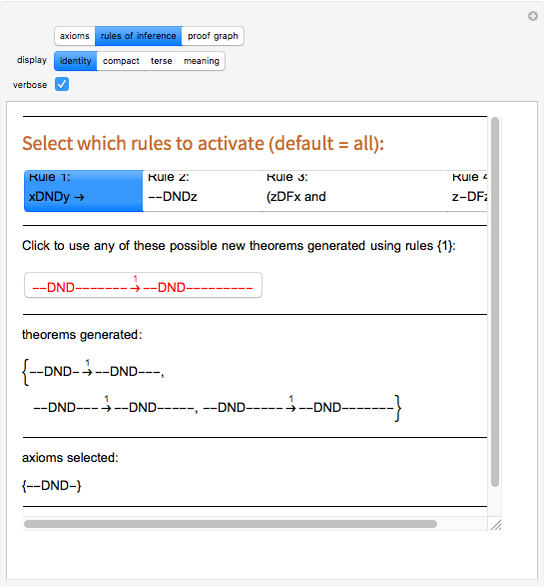
Next click the tab for the "rules of inference" page. This is where most of your exploration will take place. Given your choice of axiom(s), certain theorems can be generated from the rules of inference (or rules of production). It might be good to toggle off all except Rule 1, to make it easy to understand what Rule 1 does. Any possible theorems based on your axiom(s) and rule(s) are shown as red buttons: click a button to add that theorem to your collection. Note that each theorem "proved" (generated) can immediately be used to generate still other theorems, and the red buttons change to reflect this. For example, based on the axiom "2DND1", Rule 1 allows us to generate "2DND3", and from that "2DND5", and from that "2DND7", etc. A similar string of theorems results from applying Rule 1 iteratively to the axioms "3DND1", "3DND2", and so on. Below the rule buttons and the red theorem generation buttons, for the user's reference are the list of theorems generated so far, the list of axioms originally chosen, and a button to clear the theorem list and restart.

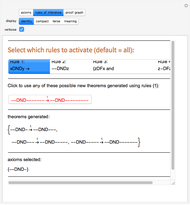
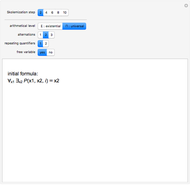
Snapshot 2: the rules of inference page with axiom "--DND-" and a sequence of three generated theorems, all shown in identity form, verbose mode

Lower controls: Possible display modes are identity (hyphen strings), compact (hyphen strings replaced by numbers), terse (DND replaced by the mathematical symbol for its meaning), and meaning (all symbols replaced by English sentences). These apply to axioms and theorems alike. If "verbose" mode is active, theorems are shown in the format "old theorem" "new theorem", with the number of the rule used shown over the arrow. Otherwise only the new theorem is shown.

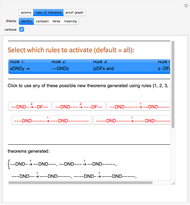
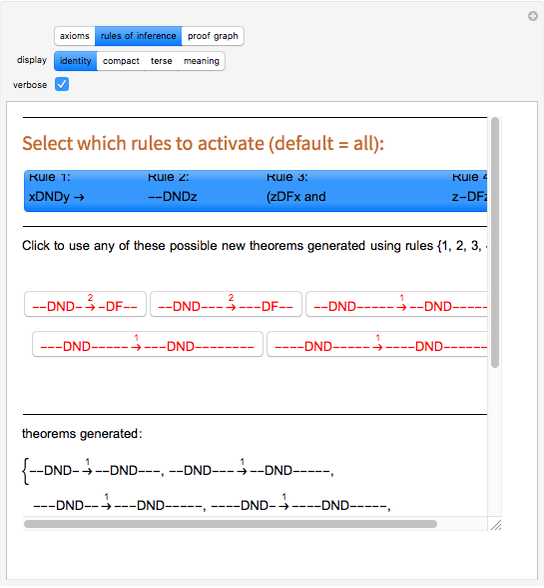
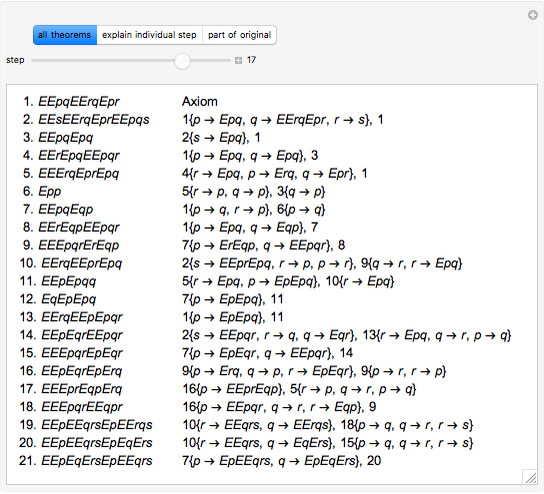
Snapshot 3: the rules of inference page with three axioms and various generated theorems ending in "P-----", all shown in identity form, verbose mode

Snapshot 4: the rules of inference page with three axioms and various generated theorems ending in "P5", all shown in compact form, verbose mode turned off

The "proof graph" page shows the logic of the proofs built on the previous pages: which theorems are proved from which axioms and theorems. If verbose mode is on, axioms and theorems are displayed on the nodes of the graph, and rule numbers on the arrows (edges) of the graph. If verbose mode is off, these labels are only displayed if the user points at the node or edge with the mouse. Axioms and theorems are displayed in the currently selected display form.

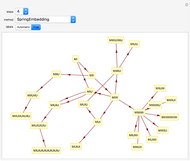
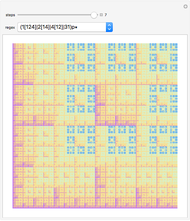
Snapshot 5: the proof graph page showing the proof of "P5" with all necessary axioms and intermediate theorems, all shown in compact form, verbose mode turned on

Snapshot 6: the proof graph page showing the proofs of "P3", "P5", "P7", and "P11" with all necessary axioms and intermediate theorems, verbose mode turned off: hover the mouse pointer over the various nodes of the graph to identify them

Meaning of the System

This Demonstration allows the user to easily interact with the primality formal system (PFS), introduced by Douglas Hofstadter in Chapter 3 of [1], as an example method of capturing primality in a formal, mechanical way.

Note that although the tq-system generated proofs that non-prime positive integers are composite, while that system will eventually generate such a proof for any composite number, it cannot encapsulate primality. (Absence of proof is not proof of absence.) PFS does guarantee to verify the primality of any given prime number… eventually. The system is characterized by its axioms and theorem production rules listed below (where "", "", 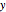and "" are strings composed of hyphens only):

Axiom schema: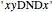

Rule 1:

Rule 2:

Rule 3: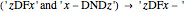

Rule 4:

One additional axiom: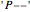

Hofstadter makes no secret about the intent of the system, so neither will we here.

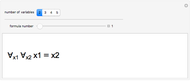
The axiom schema or pattern "means" [1] that any number greater than does not divide .

Rule 1 means that if does not divide 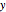, then x does not divide .

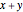The axiom schema and Rule 1 formalize the concept of "does not divide", generating axioms and theorems of form 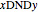for all pairs of positive numbers such that does not divide evenly into .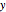

Rule 2 means that if 2 does not divide , then is divisor free up to 2.

Rule 3 means that if is divisor free up to and if does not divide , then is divisor free up to .

Rule 4 means that if 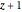is divisor free up to then 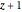is prime.

This formalizes the concept of primality, generating theorems of the form 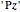for numbers if is divisor free up to .

The additional axiom means that 2 is prime: this is needed since the preceding axioms and rules will never prove it.

Challenges

1. Characterize the set of intermediate theorems of type 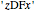necessary to generate the theorem 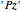. (For example, what 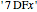theorems are needed to generate ?)

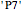2. Characterize the minimum set of axioms needed to prove .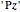

3. Characterize the minimum set of intermediate theorems necessary to generate the theorem 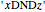from an axiom of the form 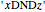. (For example, to generate the theorem 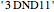from the axiom 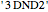, you need to generate intermediate theorems 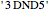and .)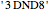

4. What is the minimum set of axioms and intermediate theorems necessary to generate the proofs 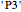, , 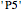, , 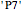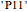or 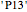? (Hint: some of them are shown in the snapshots!)

CAUTION: Spoiler Alert! You may want to consider the previous challenges and play with the system before reading on….

5. Prove that to generate 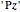(if is indeed prime) 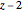axioms are needed, namely: 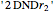, , 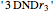…, , 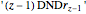where .

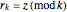6. Prove that to generate 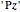(if is indeed prime), 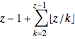intermediate theorems are needed.

7. Clearly it is possible to design an algorithm that starts with one or more axioms in a "theorem bucket" (collection) and then iterates, at each step (a) generating all possible theorems that can be produced by applying the four rules of inference to all theorems in the bucket; and (b) adding one or more new axioms to the bucket. Identify a good choice of which and how many axioms to start with and to add at each step, so that axioms are made available at approximately the step at which they are needed to generate the sequence of 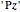theorems efficiently.

Reference:

[1] D. R. Hofstadter, Gödel, Escher, Bach: An Eternal Golden Braid, New York: Basic Books, 1979.