Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Modular Multiplication on a Circle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

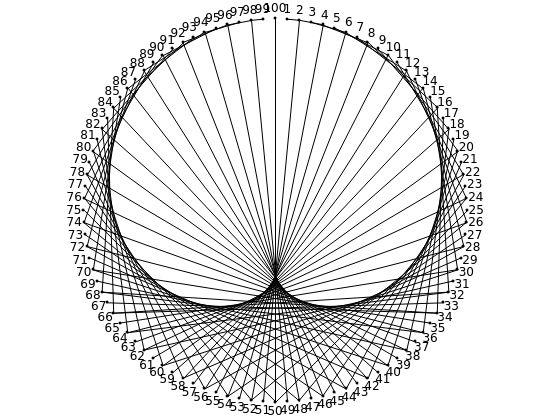
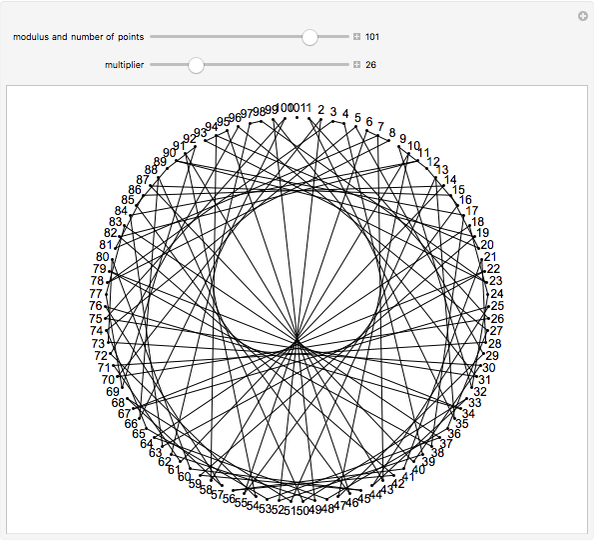
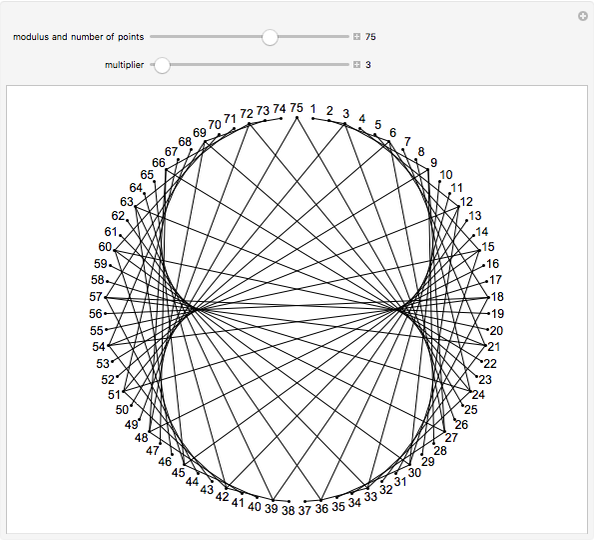
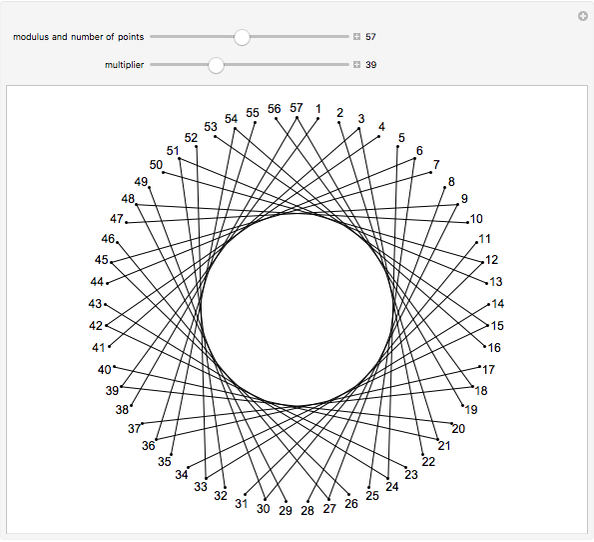
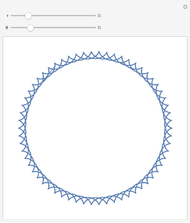
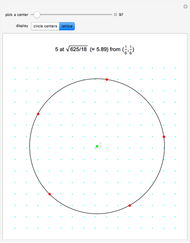
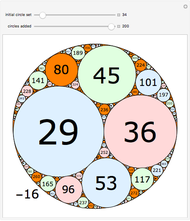
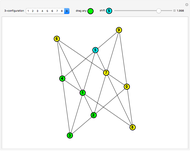
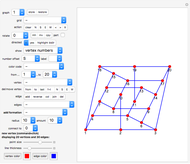
Multiply the positive integers by 3 (mod 10) to get the repeating sequence . This Demonstration connects the starting values to the ending values for a chosen modulus and multiplier .

[more]

With multipliers of 2, 3, and 6, cusped epicycloids develop—the cardioid, nephroid, and ranunculoid. Other patterns develop with other moduli and multipliers.

[less]

Contributed by: Ed Pegg Jr (November 2015)
Open content licensed under CC BY-NC-SA

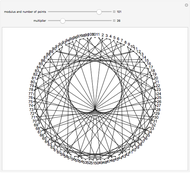
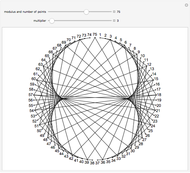
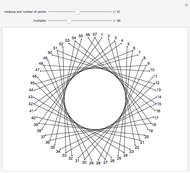
Snapshots

Details

References

[1] B. Polster. Times Tables, Mandelbrot and the Heart of Mathematics [Video]. (Nov 11, 2015) www.youtube.com/watch?v=qhbuKbxJsk8.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send