Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

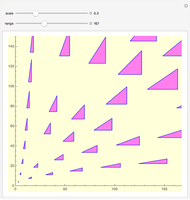
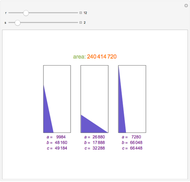
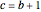Generating Near-Isosceles Pythagorean Triples

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

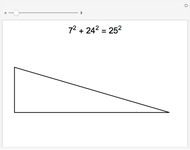
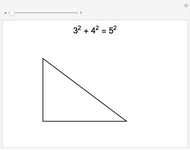
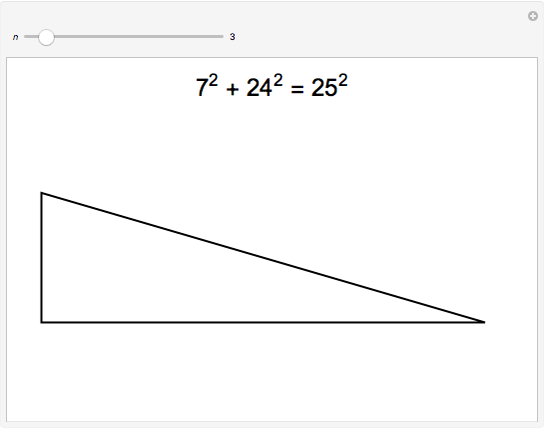
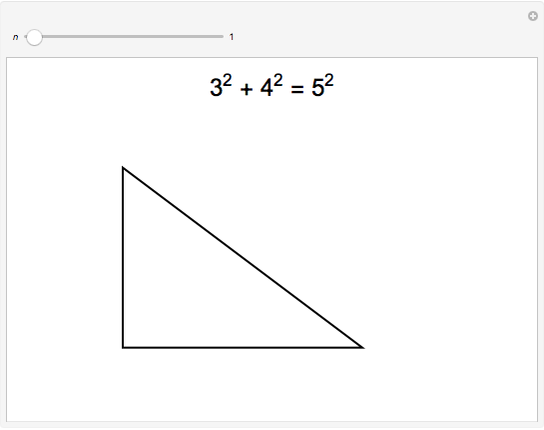
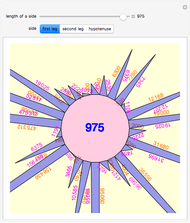
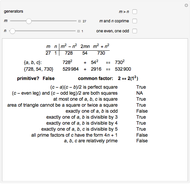
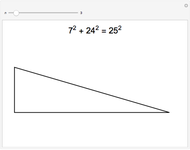
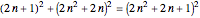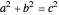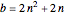
The identity is of the form of a Pythagorean triple , with , 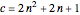. [more]

Since , this evidently represents a near-isosceles right triangle.

This Demonstration shows this result for selected values of from 1 to 20.

[less]

Contributed by: S. M. Blinder (January 2019)
Open content licensed under CC BY-NC-SA

Details

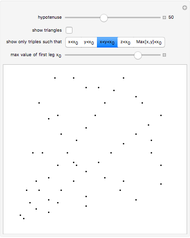
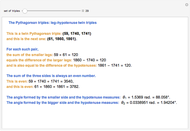
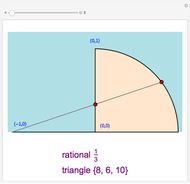
A somewhat similar formula for triples, known to Pythagoras and the Babylonians, is given by

.

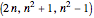Reference

[1] E. W. Weisstein. "Pythagorean Triple" from Wolfram MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/PythagoreanTriple.html (Wolfram MathWorld).

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send