Monte Carlo Valuation of an Option

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
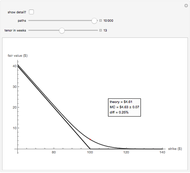
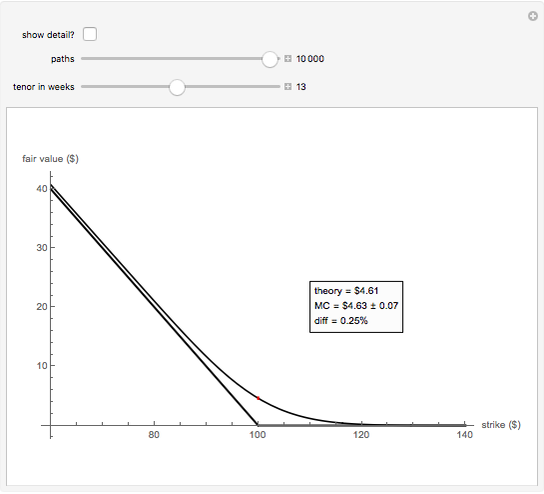
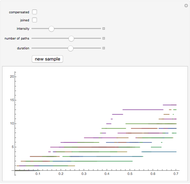
Perspective: The call option price is shown as a function of the strike price. The black line comes from the Black-Scholes theory while the red bar (95% confidence band) is a Monte Carlo estimate. The controls are the number of Monte Carlo price paths and the tenor of the option in weeks.
[more]
Contributed by: N. T. Gladd (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
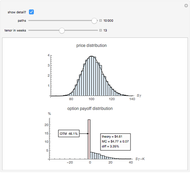
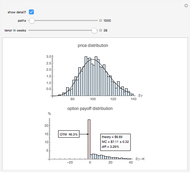
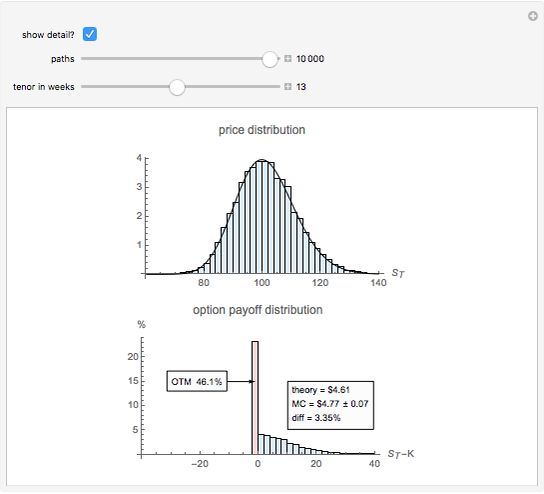
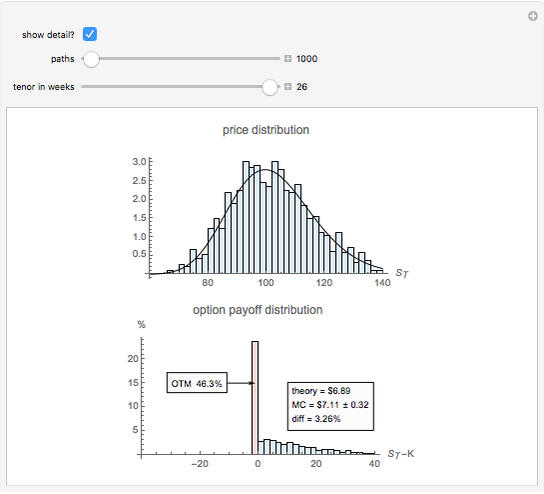
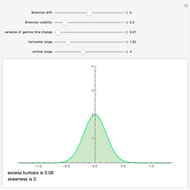
Monte Carlo simulation is a workhorse method for valuing contemporary financial derivatives and structured products. This Demonstration illustrates how simulation can be used to estimate the fair value of a simple European-style call option on a stock.
A European-style call option is the right, but not the obligation, to "call" for a stock at a specified "strike" price 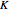 at a specified time
at a specified time 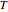 called the "tenor". If the stock price
called the "tenor". If the stock price 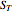 at time
at time 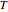 is such that
is such that 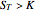 , the option holder "exercises" and collects
, the option holder "exercises" and collects  from the seller of the option. If
from the seller of the option. If 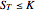 , the option expires worthless or "out of the money". In either case the seller of the option collects a fee called the "premium" for entering into the agreement. It was Fischer Black, Myron Scholes, and Robert C. Merton who, in 1973, determined the appropriate premium or "fair value" of this option—the value under which the buyer and seller should enter an agreement. This work, which was awarded the Nobel prize in 1997, spawned an explosion of financial activity that continues to this day. A remarkable feature of this so-called "arbitrage-free pricing theory" is that both the buyer and seller will agree on the fair value of an option on a stock, even if they have opposite views on whether the price of the stock will go up or down.
One consequence of this theory is that the fair value of an option is the discounted expected value of the option payoff
, the option expires worthless or "out of the money". In either case the seller of the option collects a fee called the "premium" for entering into the agreement. It was Fischer Black, Myron Scholes, and Robert C. Merton who, in 1973, determined the appropriate premium or "fair value" of this option—the value under which the buyer and seller should enter an agreement. This work, which was awarded the Nobel prize in 1997, spawned an explosion of financial activity that continues to this day. A remarkable feature of this so-called "arbitrage-free pricing theory" is that both the buyer and seller will agree on the fair value of an option on a stock, even if they have opposite views on whether the price of the stock will go up or down.
One consequence of this theory is that the fair value of an option is the discounted expected value of the option payoff
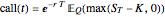
where  is the risk-free interest rate. The symbol
is the risk-free interest rate. The symbol 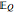 denotes expectation (or average) for a particular distribution of prices. In more detail
denotes expectation (or average) for a particular distribution of prices. In more detail

where 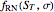 is the "risk-neutral" distribution of stock prices at time
is the "risk-neutral" distribution of stock prices at time 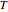 , a quantity that also depends on the volatility
, a quantity that also depends on the volatility  of the stock and the interest rate
of the stock and the interest rate  . For the case considered in this Demonstration, the risk-neutral price distribution is the lognormal distribution
. For the case considered in this Demonstration, the risk-neutral price distribution is the lognormal distribution
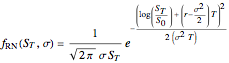
For this simple example, there is no need to resort to Monte Carlo simulation to value the integral. However, contemporary finance deals with much more complicated instruments for which there is no closed-form expression for the expectation in the first equation. Monte Carlo simulation is useful under such circumstances.
References:
http://nobelprize.org/nobel_prizes/economics/laureates/1997/
J. C. Hull, Options, Futures, and Other Derivatives, 7th ed., Upper Saddle River, NJ: Prentice Hall, forthcoming.
P. Glasserman, Monte Carlo Methods in Financial Engineering, New York: Springer, 2004.
Permanent Citation