The Poisson Process
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
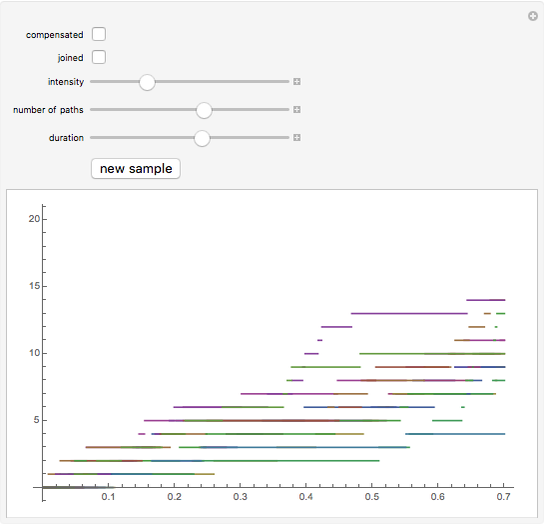
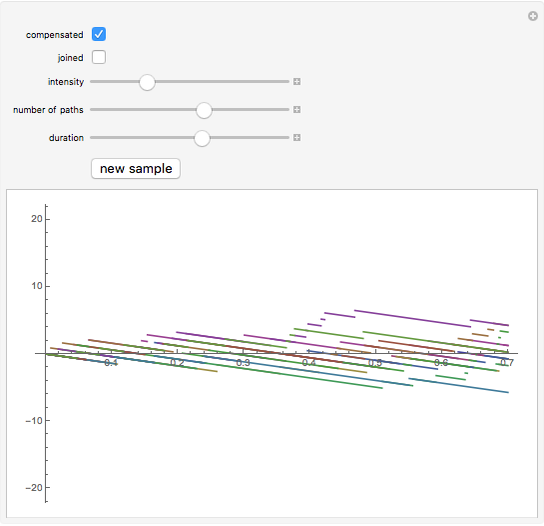
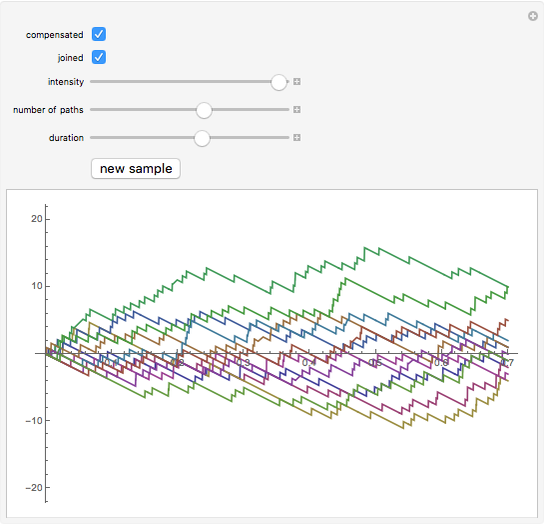
This Demonstration shows sample trajectories of a Poisson process—a fundamental example of a stochastic process with discontinuous trajectories, which is used as a building block for constructing jump processes that play an important role in modern financial modeling. You can vary the intensity of the jumps, the duration, whether the trajectories should be connected, and whether an ordinary Poisson process or a "compensated" one should be displayed.
Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Poisson process is one of the two most fundamental stochastic processes in continuous time financial modelling, the other being Brownian motion, with which it shares a number of common properties (both are examples of a Levy process). In this Demonstration two kinds of Poisson processes are shown: an ordinary one and one that is "compensated". The compensated Poisson process is a martingale with expected value 0. As the intensity of jumps increases, the compensated Poisson process approximates a Brownian motion (this follows from the Donsker invariance principle). Making the plot joined and choosing a high value for the intensity makes the trajectories resemble those in standard simulations of Brownian motion.
R. Cont, P. Tankov, Financial Modelling with Jump Processes, Boca Raton, London, New York, Washington, D.C: Chapman & Hall, 2004.
Permanent Citation
"The Poisson Process"
http://demonstrations.wolfram.com/ThePoissonProcess/
Wolfram Demonstrations Project
Published: March 7 2011
The Return Distribution of the Variance Gamma Process
Andrzej Kozlowski
Correlated Wiener Processes
Andrzej Kozlowski
Two Jump Diffusion Processes
Andrzej Kozlowski
Simulating the Poisson Process
Heikki Ruskeepää
Merton's Jump Diffusion Model
Andrzej Kozlowski
Brownian Bridge
Andrzej Kozlowski
Correlated Gamma Variance Processes with Common Subordinator
Andrzej Kozlowski
Generalized Hyperbolic Distribution
Andrzej Kozlowski
Density of the Kou Jump Diffusion Process
Andrzej Kozlowski
The Normal Inverse Gaussian Lévy Process
Piotr Teklinski, Piotr Wroblewski, and Andrzej Kozlowski
-
The Black-Scholes European Call Option Formula Corrected Using the Gram-Charlier Expansion
Andrzej Kozlowski -
Option Prices in the Kou Jump Diffusion Model
Andrzej Kozlowski -
The Polar and Bipolar of a Convex Polytope
Andrzej Kozlowski -
Two Jump Diffusion Processes
Andrzej Kozlowski -
The Vieta Mapping for the Coxeter Group A_2
Andrzej Kozlowski -
The Bifurcation Set of the Space of Smooth Real Functions
Andrzej Kozlowski -
The Swallowtail Singularity
Andrzej Kozlowski -
Singularities of an Ellipsoidal Wave Front
Andrzej Kozlowski -
Nonuniqueness of Option Pricing Under the Meixner Model
Andrzej Kozlowski -
Coin Machine
Andrzej Kozlowski -
A Mean-Reverting Jump Diffusion Process
Andrzej Kozlowski -
Standard American and European Options
Andrzej Kozlowski -
Density of the Kou Jump Diffusion Process
Andrzej Kozlowski -
The Meixner Process
Andrzej Kozlowski -
Fitting the Meixner Distribution to S&P 500 Returns
Andrzej Kozlowski -
Simple Graphs and Their Binomial Edge Ideals
Andrzej Kozlowski -
The Eneström-Kakeya Bounds for Roots of a Polynomial with Positive Coefficients
Andrzej Kozlowski -
Newton Polygon and Branching of Algebraic Curves
Andrzej Kozlowski -
Counting the Number of Roots of Transcendental Functions in Bounded Regions Using Winding Numbers
Andrzej Kozlowski -
The Space of Inner Products
Andrzej Kozlowski