Orthocentre d'un triangle inscrit dans une hyperbole (French)

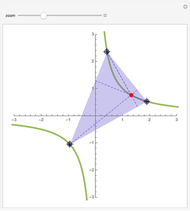
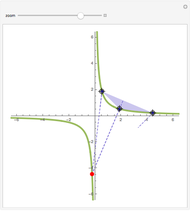
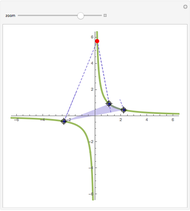
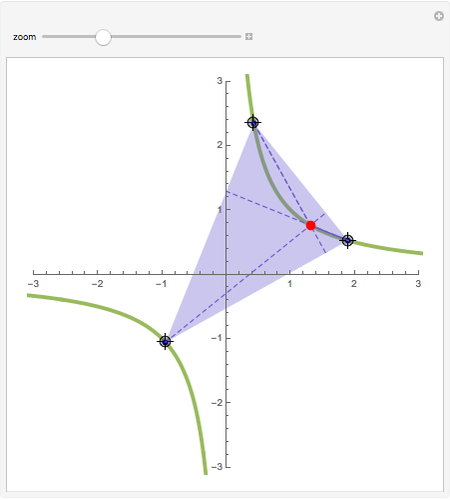
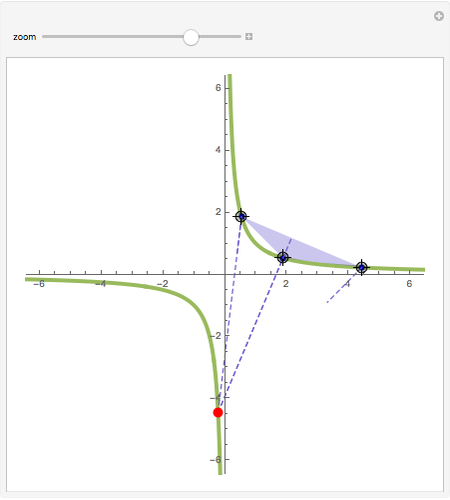
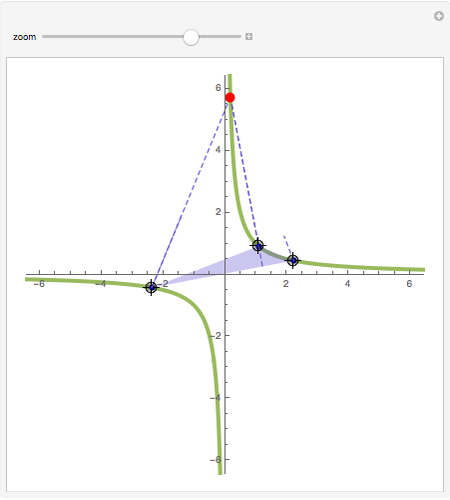
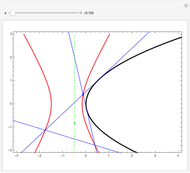
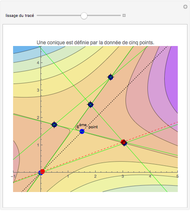
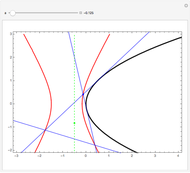
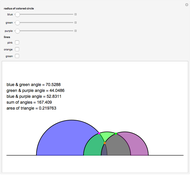
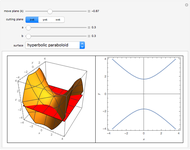
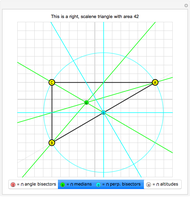
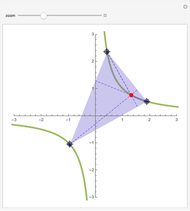
L'orthocentre du triangle formé par trois points d'une hyperbole est encore sur l'hyperbole. Une "preuve" intuitive consiste à considérer l'ensemble des hyperboles équilatères passant par trois points: dans l'espace projectif de dimension cinq des coniques, elles satisfont quatre conditions linéaires, donc leur ensemble est une droite, i.e., c'est un faisceau de coniques passant par quatre points. Ce quatrième point, en plus des trois sommets du triangle, en est l'orthocentre (on le voit avec une conique dégénérée dans le faisceau).