PID Control of a Tank Level

The dynamic behavior of the tank height (in meters) is governed by the following ODE:

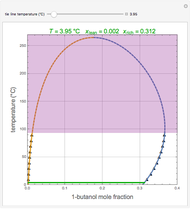
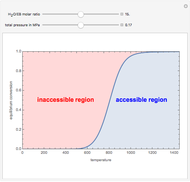
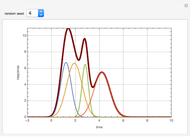
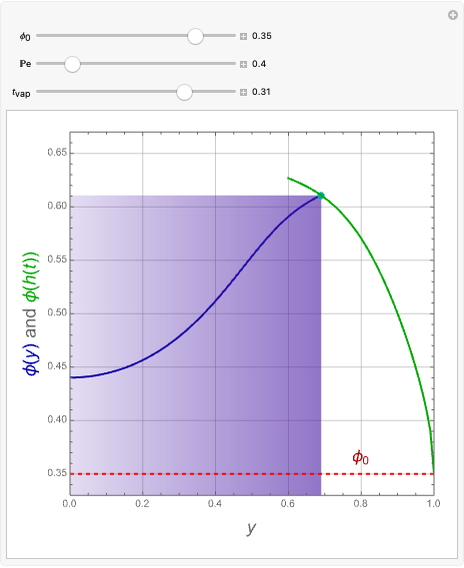
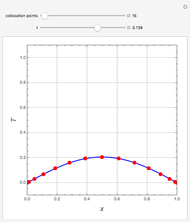
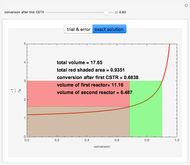
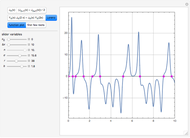
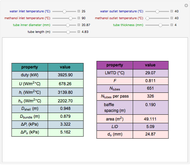
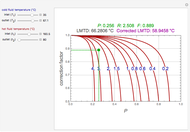
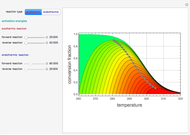
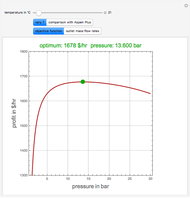
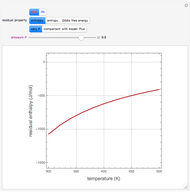
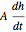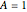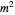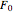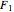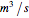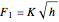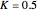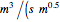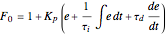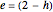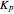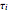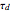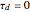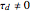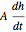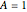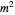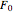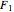= where is the tank area in , and are the inlet and outlet flow rates (expressed in 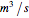), respectively. Initially the tank height is equal to 0.1 meter.

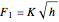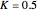The flow equation is given by: where is the valve constant expressed in ).

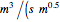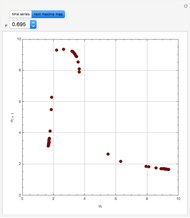
The setpoint for the tank height is chosen to equal 2 meters.

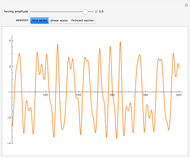
The inlet flow rate is varied in order to achieve the desired setpoint value using a P, PI, or PID (proportional–integral–derivative) control: 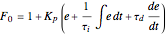, where 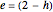is the error, 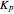is the proportional gain, and 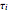and 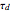are the integral and differential time constants, respectively.

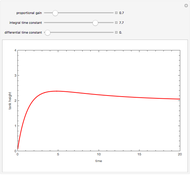
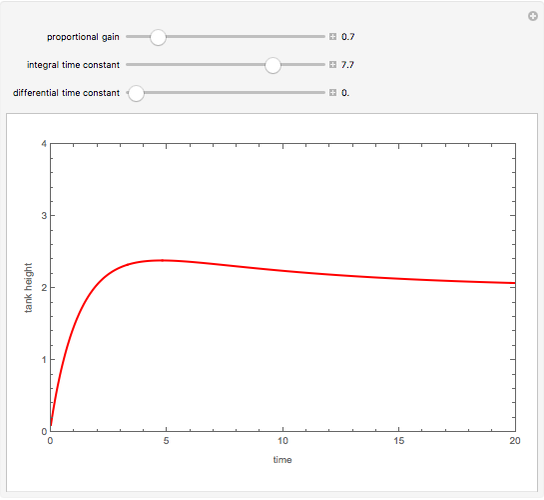
For large 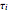and 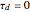, the control simplifies to the usual proportional control, which is usually characterized by a small offset value (i.e., the final steady-state height is not exactly equal to the setpoint value).

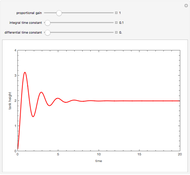
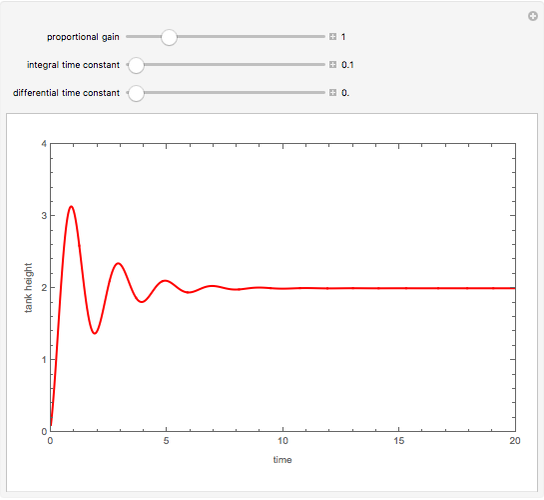
PI control is achieved when 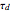is taken to be zero. PI control can show an overshoot and dumped oscillations around the setpoint. No offset is observed and the final steady-state tank height is exactly equal to the setpoint value.

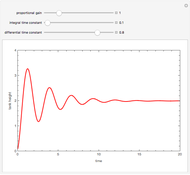
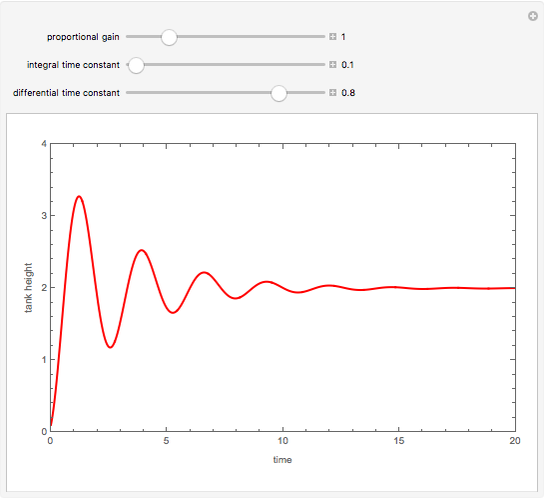
In the most general case, when 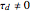and 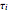is not too large, one gets PID control of the tank height.