Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

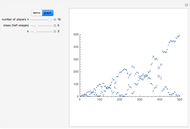
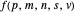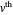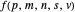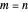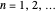Pascal-like Triangle Made from a Card Game

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

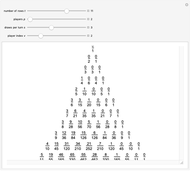
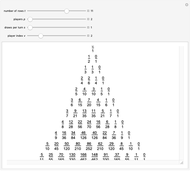
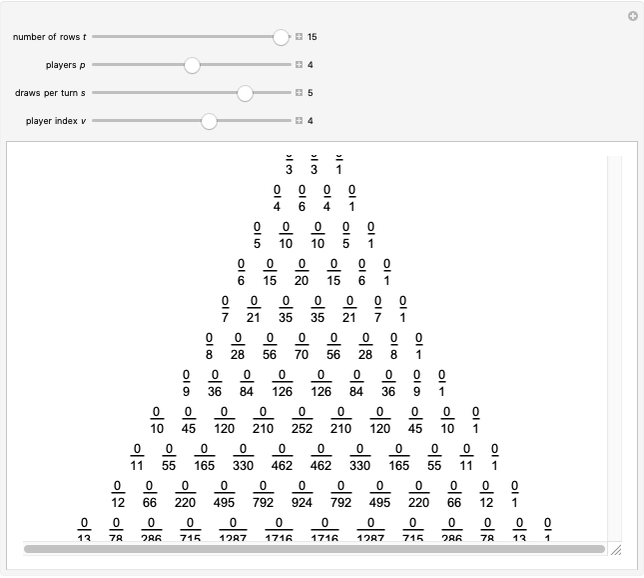
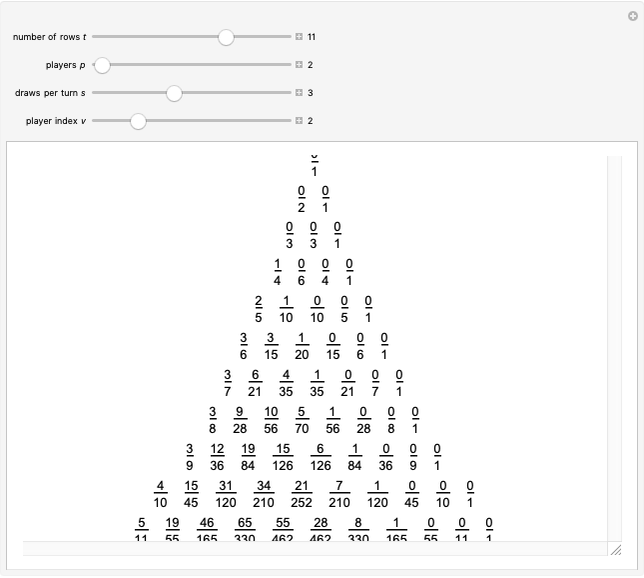
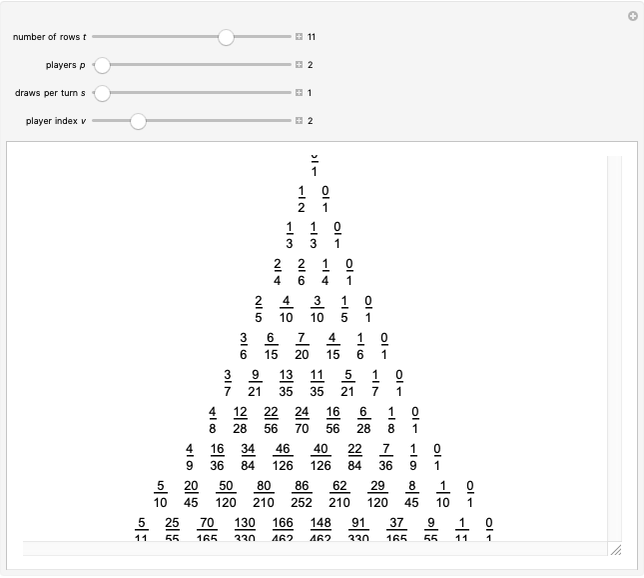
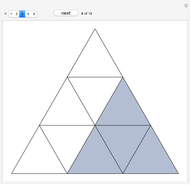
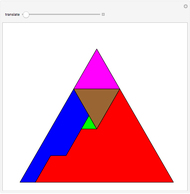
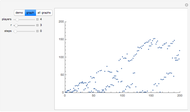
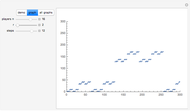
Let , , 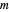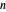and be fixed positive integers, with 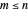. There are 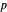players. Each draws cards in turn from a pile of cards containing 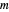red cards and 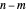white cards. A player immediately loses the game after drawing a red card. This game is mathematically equivalent to a Russian roulette game in which 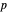players take turns.

[more]

Let be the probability that the player loses the game. Then for fixed positive integers , and , the set of denominators and numerators of for , , have a very similar pattern to the pattern of Pascal's triangle.

[less]

Contributed by: Ryohei Miyadera (April 2019)
Open content licensed under CC BY-NC-SA

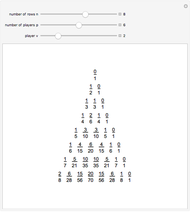
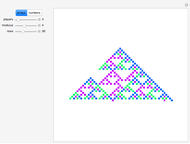
Snapshots

Details

This generalizes the author's Demonstration "Pascal-like Triangles Made from a Game", and the result generalizes results published by Miyadera [1,2].

References

[1] H. Matsui, D. Minematsu, T. Yamauchi and R. Miyadera, "Pascal-like Triangles and Fibonacci-like Sequences," The Mathematical Gazette, 94(529), 2010 pp. 27–41. doi:10.1017/S0025557200007129.

[2] R. Miyadera et al., "Pascal-Like Triangles and Fibonacci-Like Sequences," The 20th Japan Conference on Discrete and Computational Geometry, Graphs, and Games (JCDCG3 2017), Tokyo University of Science, August, 2017.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send