Fault-Free Tilings

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
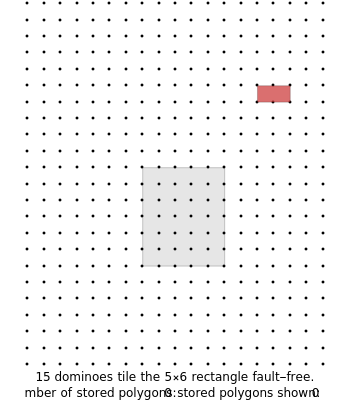
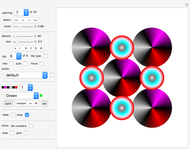
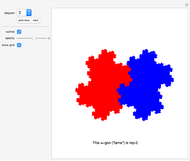
A tiling is called fault free if it has no "breaking line" (a straight line that does not go through the interior of any tile).
[more]
Contributed by: Karl Scherer (March 2011)
Additional contributions by: David Klarner and Michael Reid
Open content licensed under CC BY-NC-SA
Snapshots
Details
To place a tile, move the sample to the position you want, then use the slider for the proper rotation, and finally click the "store new tile" button.
The first three examples in this Demonstration deal with the problem of packing rectangles into a rectangular box. In 1980 the author showed (in the Journal of Recreational Mathematics) that the (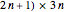 box is the smallest box that allows a fault-free packing of
box is the smallest box that allows a fault-free packing of 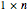 tiles.
tiles.
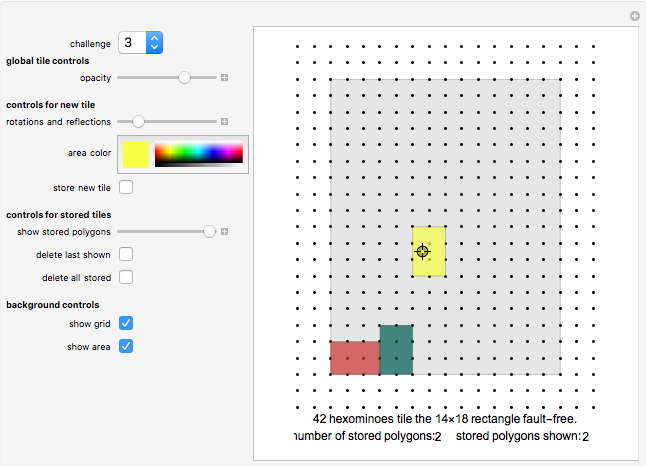
The author also showed how in general a ( box can be packed with
box can be packed with 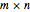 tiles, and he conjectured that this is indeed the smallest box of this type for any numbers
tiles, and he conjectured that this is indeed the smallest box of this type for any numbers  and
and  with no common divisor. This interesting result answered a question posed by Martin Gardner.
with no common divisor. This interesting result answered a question posed by Martin Gardner.
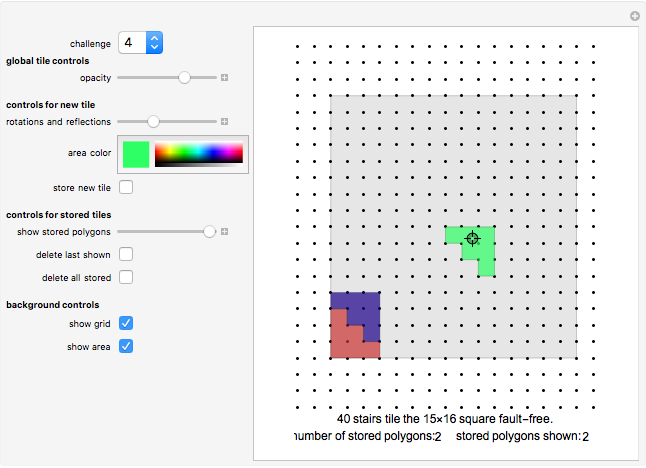
Example 4 is taken from the author's book A Puzzling Journey to the Reptiles and Related Animals, 1987, published privately.
Reference: M. Gardner, New Mathematical Diversions from Scientific American, New York: Simon and Schuster, 1966.
Permanent Citation