Projecting a Circle on a Sphere to an Enclosing Cylinder

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
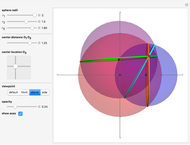
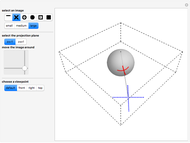
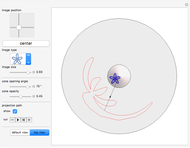
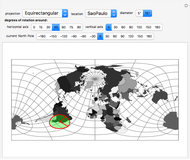
A cylindrical projection maps points on a sphere to a cylinder wrapped around the sphere at its equator.
[more]
Contributed by: Erik Mahieu (February 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The transformation formulas used in this Demonstration are based on the Mathematica built-in function ToSphericalCoordinates and the conversion formulas in [1, 2].
For the equidistant projection, the following mapping is used to convert the Cartesian coordinates of a point on the unit sphere to the corresponding point on the cylinder wrapped around it:
 .
.
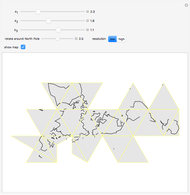
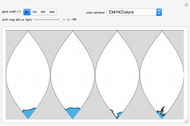
The equidistant projection to a plane uses the following mapping to convert the Cartesian coordinates of a point on the unit sphere to the corresponding point on the 2D plane:  .
.
For the equal area projection, the following mapping is used to convert the Cartesian coordinates of a point on the unit sphere to the corresponding point on the cylinder wrapped around it:  .
.
The equal-area projection to a plane uses the following mapping to convert the Cartesian coordinates of a point on the unit sphere to the corresponding point on the 2D plane:  .
.
References
[1] E. W. Weisstein. "Cylindrical Equidistant Projection" from MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/CylindricalEquidistantProjection.html (Wolfram MathWorld).
[2] E. W. Weisstein. "Cylindrical Equal-Area Projection" from MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/CylindricalEqual-AreaProjection.html (Wolfram MathWorld).
Permanent Citation