Proportional-Integral Control of Batch Rectification Process

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
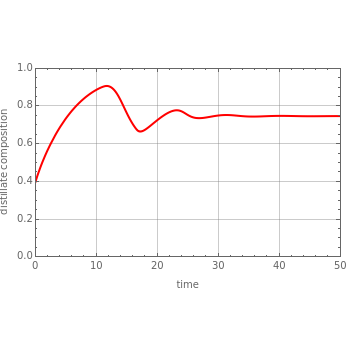
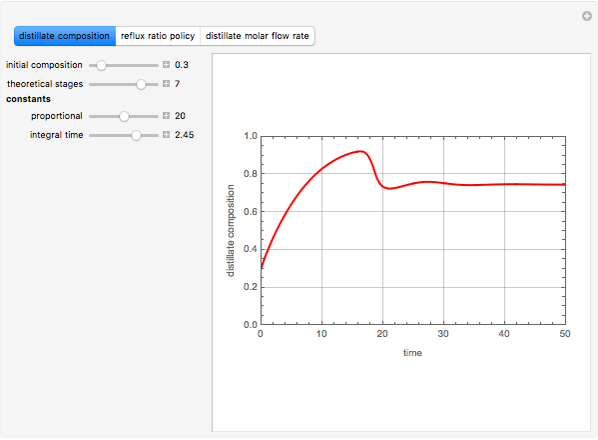
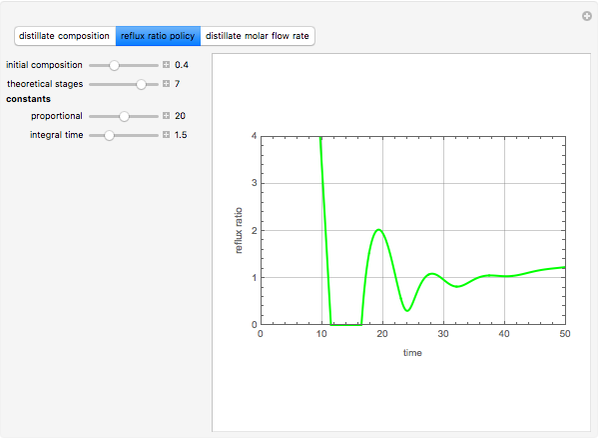
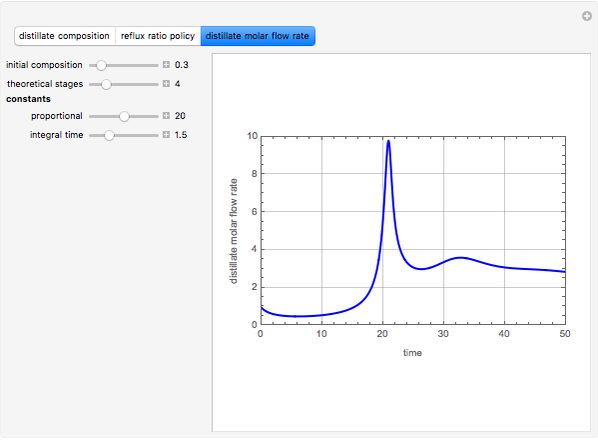
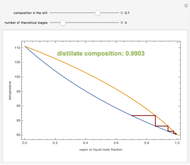
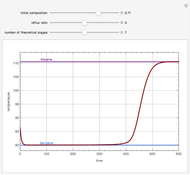
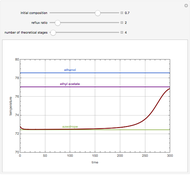
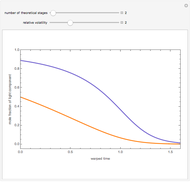
Consider an ideal binary mixture of benzene and toluene at 760 mmHg. This mixture is to be separated with a batch rectification system having a user-set number of theoretical stages. The column and the still are initially filled with a composition in mole % benzene that can also be set. The reflux ratio is adjusted using a PI (proportional-integral) controller so that the distillate purity is a constant 75 mole % benzene. This Demonstration displays the distillate composition, the reflux ratio, and the distillate molar flow rate versus time. It is clear from the results that as the still gets depleted in the most volatile compound (the benzene), the reflux ratio must be increased in order to maintain the distillate purity specification. Increased reflux ratios also correspond to smaller distillate molar flow rates as can be seen from the snapshots.
Contributed by: Housam Binous and Ahmed Bellagi (March 2011)
Open content licensed under CC BY-NC-SA