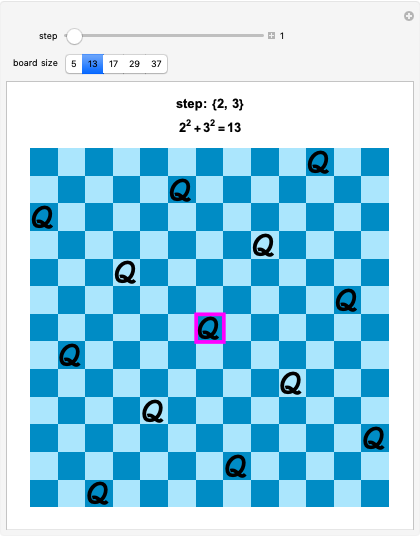
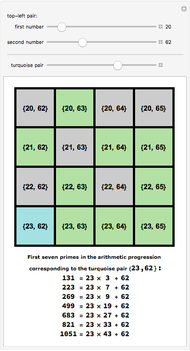
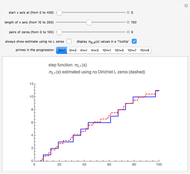
Pseudoprime
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Fermat's little theorem (FLT) states that for any prime number 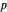 and coprime base
and coprime base 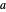 ,
, 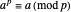 . If this congruence fails, then
. If this congruence fails, then  cannot be prime. Using FLT as a primality test seems promising because it distinguishes primes from nonprimes in many cases. For example,
cannot be prime. Using FLT as a primality test seems promising because it distinguishes primes from nonprimes in many cases. For example, 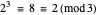 ,
,  ,
, 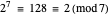 ,
, 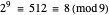 , so 9 isn't prime, and so on. This primality test works up to
, so 9 isn't prime, and so on. This primality test works up to 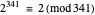 , but
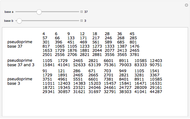
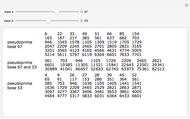
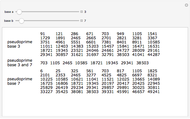
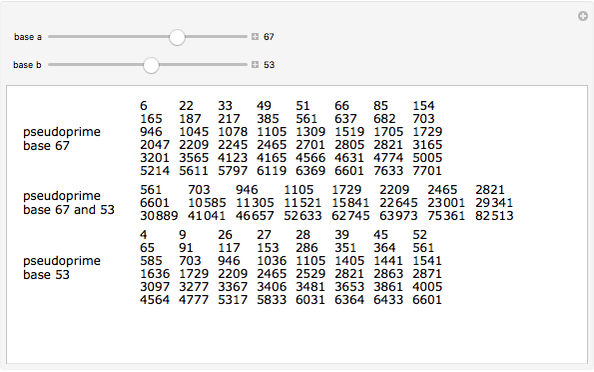
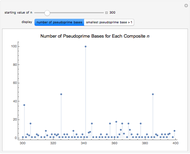
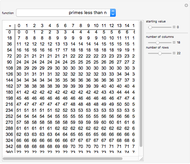
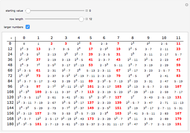
, but 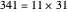 . A pseudoprime like 341 is a composite number that passes a primality test. Different bases lead to different pseudoprimes.
. A pseudoprime like 341 is a composite number that passes a primality test. Different bases lead to different pseudoprimes.
Contributed by: Ed Pegg Jr (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation