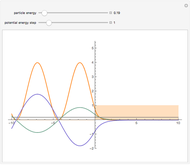
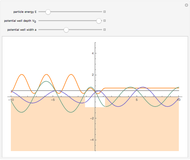
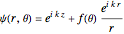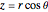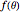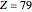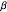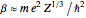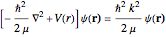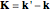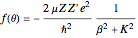This Demonstration outlines a quantum-mechanical computation for the scattering of alpha particles from heavy atoms, known as Rutherford scattering. Quite remarkably, the result for the differential cross section  agrees perfectly with that computed using classical scattering theory, although the complex scattering amplitude
agrees perfectly with that computed using classical scattering theory, although the complex scattering amplitude 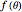 does contain a complex factor.
does contain a complex factor.
The Faxen–Holtzmark representation for scattering from a spherically symmetrical potential assumes a wavefunction 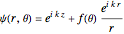 . The first term represents an incoming plane wave (note that
. The first term represents an incoming plane wave (note that 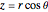 ), while the second term is an outgoing spherical wave, modulated by the scattering amplitude
), while the second term is an outgoing spherical wave, modulated by the scattering amplitude 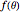 . We consider the scattering potential
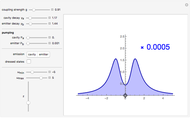
. We consider the scattering potential  , where
, where  (
(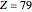 for Au, used in Rutherford's original experiments) is the atomic number of the target atom,
for Au, used in Rutherford's original experiments) is the atomic number of the target atom,  for the alpha particles, and
for the alpha particles, and 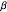 is a shielding constant due to the atomic electrons, with an approximate value
is a shielding constant due to the atomic electrons, with an approximate value 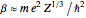 based on the Thomas–Fermi statistical model. The potential, incidentally, has the same form as a Yukawa potential for nucleon-nucleon interaction.
based on the Thomas–Fermi statistical model. The potential, incidentally, has the same form as a Yukawa potential for nucleon-nucleon interaction.
The (first-order) Born approximation is adequate for this problem. The Schrödinger equation is given by 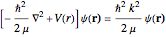 , where
, where  , the alpha particle mass, and
, the alpha particle mass, and  . Where
. Where 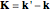 , we then find
, we then find  is the difference between the scattered and incident propagation vectors. The scattering amplitude is then given by
is the difference between the scattered and incident propagation vectors. The scattering amplitude is then given by 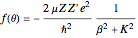 . Using
. Using  and
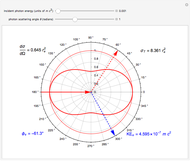
and  , we obtain the cross section
, we obtain the cross section  . With
. With  , for a pure Coulomb field, this reduces to the famous Rutherford scattering formula
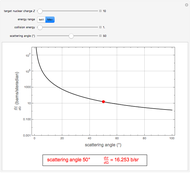
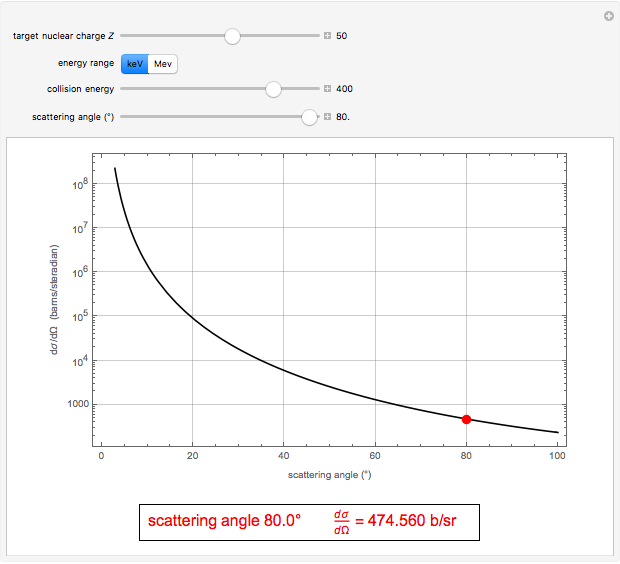
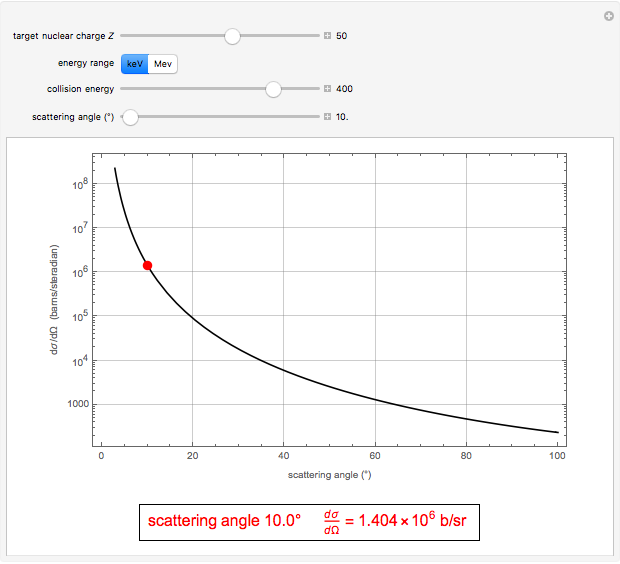
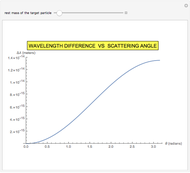
, for a pure Coulomb field, this reduces to the famous Rutherford scattering formula  . We use Gaussian cgs units for historical continuity. Because of the long range of the Coulomb potential, the scattering cross sections vary over many orders of magnitude and the total (integrated) cross section diverges.
. We use Gaussian cgs units for historical continuity. Because of the long range of the Coulomb potential, the scattering cross sections vary over many orders of magnitude and the total (integrated) cross section diverges.
[less]

 agrees perfectly with that computed using classical scattering theory, although the complex scattering amplitude
agrees perfectly with that computed using classical scattering theory, although the complex scattering amplitude 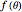 does contain a complex factor.
does contain a complex factor.