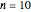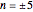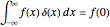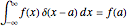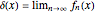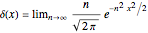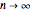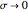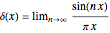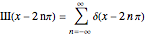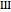The "deltafunction" was invented by P. A. M. Dirac around 1930 in order to compactly express the completeness relation in quantum mechanics. (Essentially equivalent definitions appear in earlier works of Fourier, Kirchhoff, and Heaviside.) The deltafunction is the limit of a function that grows infinitely large in an infinitesimally small region, while its integral remains normalized to 1. The deltafunction is too singular to be considered a function in the usual sense. Mathematicians have, however, accepted it as a linear functional, a "generalized function", or "distribution".
The deltafunction has computational significance only when it appears under an integral sign. Its defining relation can, in fact, be written 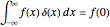 or, more generally,
or, more generally, 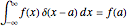 . There are a number of representations of the deltafunction based on limits of a family of functions as some parameter approaches infinity (or zero). In this Demonstration, five of these representations are illustrated. You can select the parameter
. There are a number of representations of the deltafunction based on limits of a family of functions as some parameter approaches infinity (or zero). In this Demonstration, five of these representations are illustrated. You can select the parameter  to take values from 1 to 10, on its way toward infinity.
to take values from 1 to 10, on its way toward infinity.
The most rudimentary representation is a rectangular pulse:  for
for  . Then
. Then 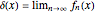 as the rectangle becomes higher and narrower.
as the rectangle becomes higher and narrower.
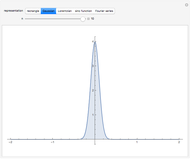
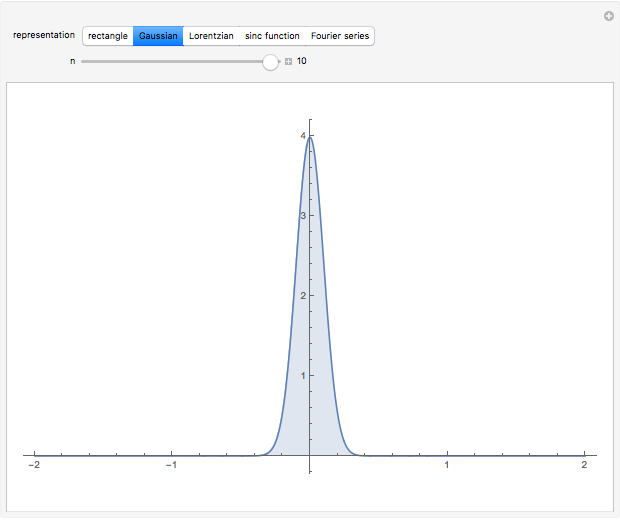
The most commonly cited representation is based on the normalized Gaussian distribution (bell-shaped curve): 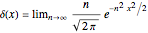 . The limit
. The limit 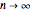 is equivalent to
is equivalent to 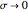 , where
, where  is the standard deviation.
is the standard deviation.
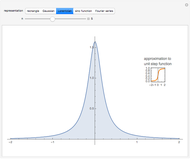
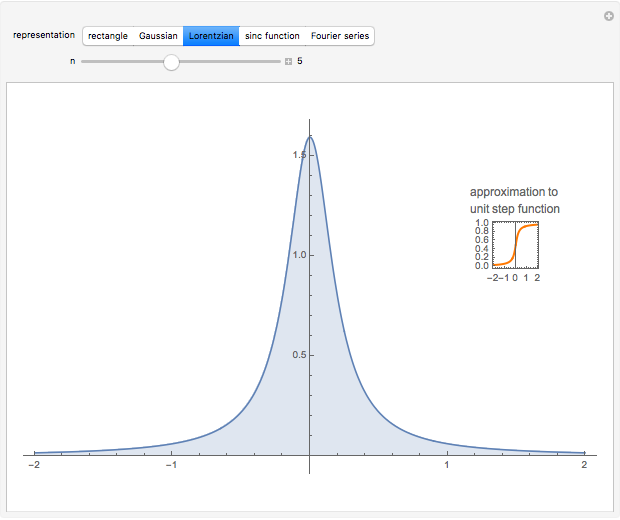
Closely analogous is the Lorentzian representation:  . The Lorentzian function is proportional to the derivative of the arctangent, shown as an inset. In the limit as
. The Lorentzian function is proportional to the derivative of the arctangent, shown as an inset. In the limit as 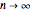 , the arctangent approaches the unit step function (Heaviside function). Thus the deltafunction represents the derivative of a step function.
, the arctangent approaches the unit step function (Heaviside function). Thus the deltafunction represents the derivative of a step function.
In quantum mechanics, one frequently encounters the representation 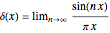 . The rapidly oscillating normalized sinc function gives an effective contribution of zero when
. The rapidly oscillating normalized sinc function gives an effective contribution of zero when  .
.
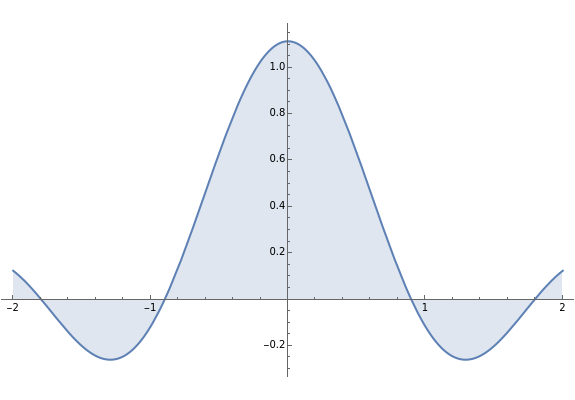
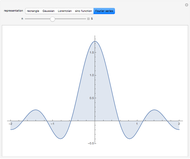
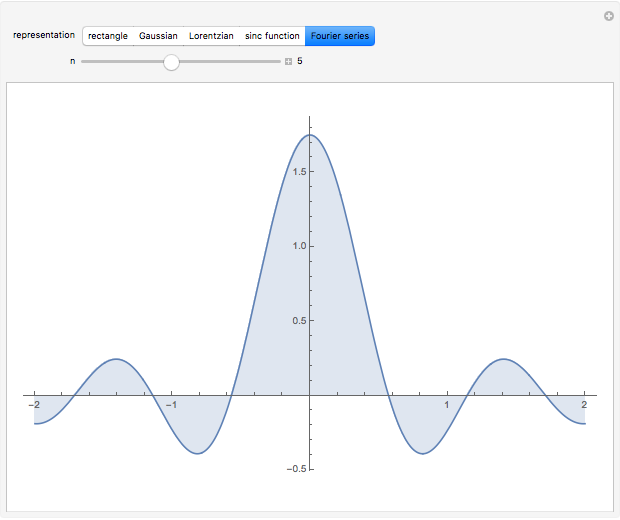
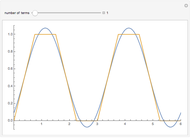
The Fourier series for the deltafunction contains unit contributions from all frequencies. A deltafunction is approached as the number of terms in the following expansion increases:  . This representation applies only in a neighborhood of the origin. More correctly, this Fourier series represents a delta comb function or shah function
. This representation applies only in a neighborhood of the origin. More correctly, this Fourier series represents a delta comb function or shah function 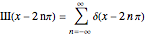 (after the Russian letter
(after the Russian letter  ).
).
[less]