Schrödinger Representations in Function Theory

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
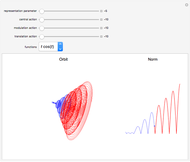
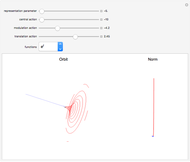
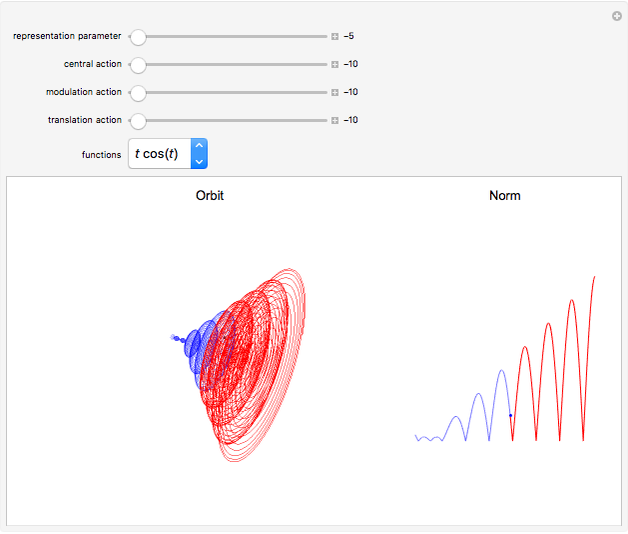
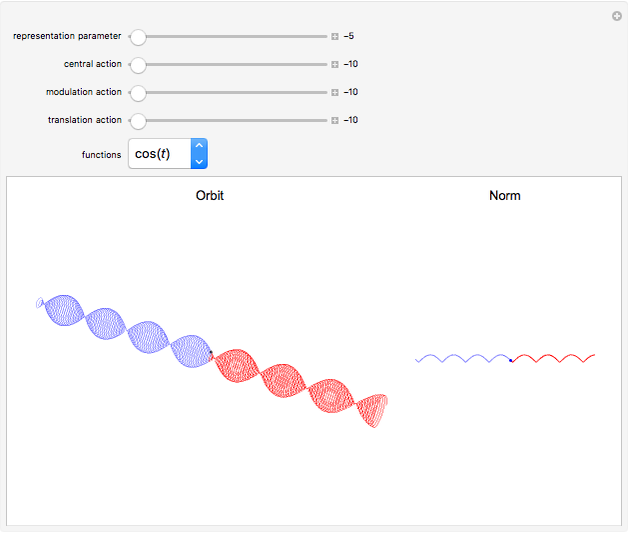
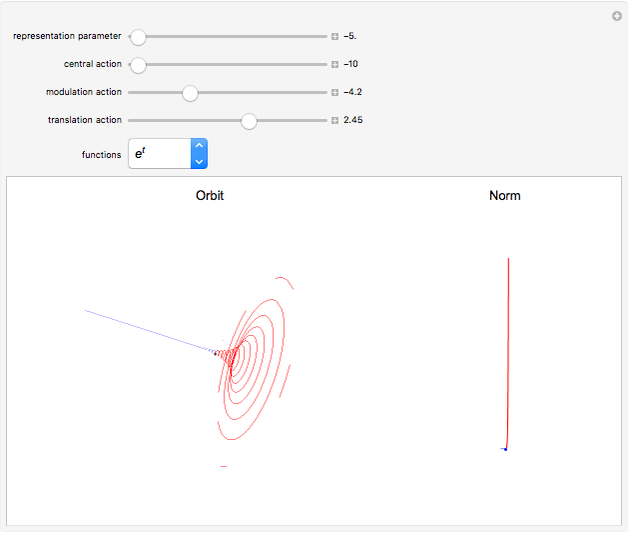
Schrödinger representations are well known in quantum mechanics, harmonic analysis, and representation theory. They are infinite-dimensional irreducible representations of the Heisenberg group. They are parametrized by linear functionals 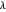 that are elements of
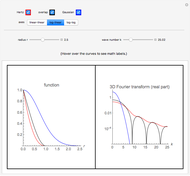
that are elements of 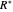 and act on functions by multiplication of characters, modulations, and translations. This Demonstration shows how these representations act on a set of functions of compact support. The function is plotted in
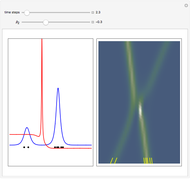
and act on functions by multiplication of characters, modulations, and translations. This Demonstration shows how these representations act on a set of functions of compact support. The function is plotted in 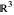 on the left; on the right is the graph of the norm of the function. The central action comes from the action of the elements related to the center of the Heisenberg group acting by the multiplication of characters. The other noncentral elements are related to modulations and translation operators.
on the left; on the right is the graph of the norm of the function. The central action comes from the action of the elements related to the center of the Heisenberg group acting by the multiplication of characters. The other noncentral elements are related to modulations and translation operators.
Contributed by: Vignon S. Oussa (DateObject[] {MonthName, Year, Day})
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation