Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Rosettes from Op Art Patterns

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

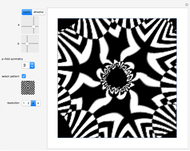
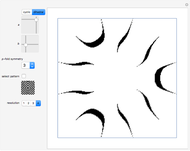
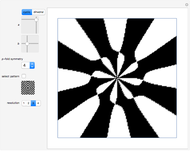
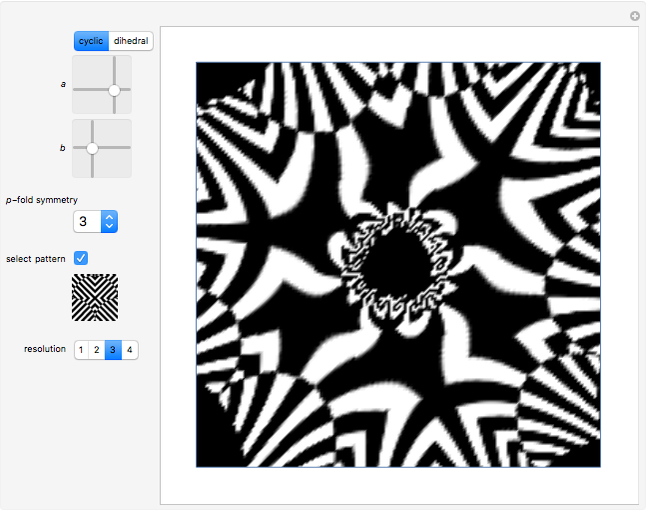
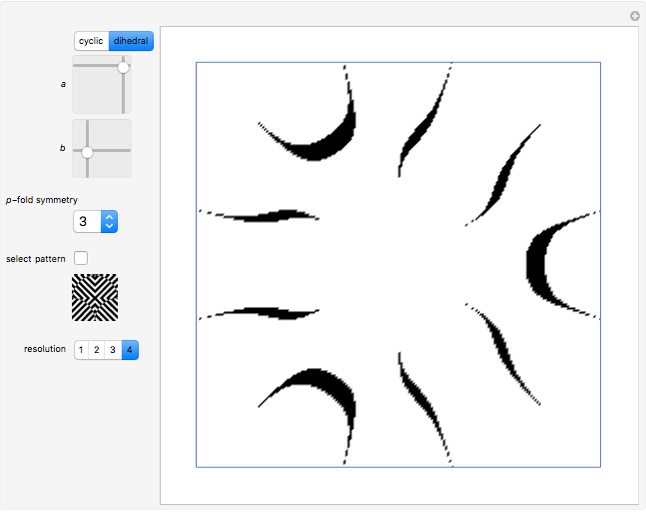
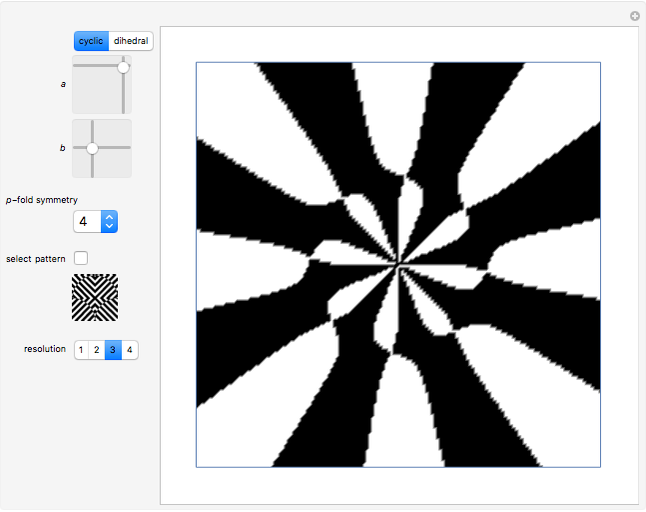
This Demonstration gives some examples of rosettes produced from various op art patterns. You can choose aspects of shape and symmetry with the functions 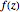and 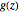that depend on the complex parameters and (defined in the Details).

Contributed by: Izidor Hafner (January 2017)
Using work by: F. A. Farris
Open content licensed under CC BY-NC-SA

Snapshots

Details

The following results are relevant:

If, in the sum 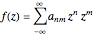, 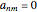unless , 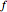is a rosette function with 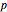-fold symmetry.

If, in the sum , 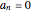unless , 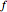is a rosette function with 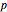-fold symmetry.

If, in the sum 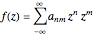, , 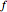is a function with mirror symmetry.

The functions 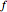(cyclic) and (dihedral) are defined by 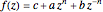and .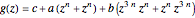

Pattern images are from [2].

References

[1] F. A. Farris, Creating Symmetry: The Artful Mathematics of Wallpaper Patterns, Princeton: Princeton University Press, 2015 pp. 40–45.

[2] S. Jablan. "Modularity in Art." (Jan 5, 2017) www.mi.sanu.ac.rs/~jablans/d3.htm.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send