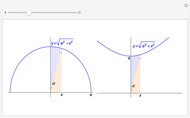
Saddle Points and Inflection Points

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
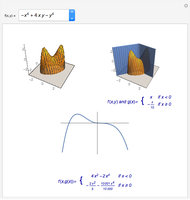
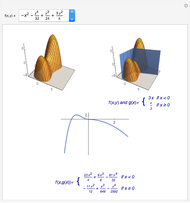
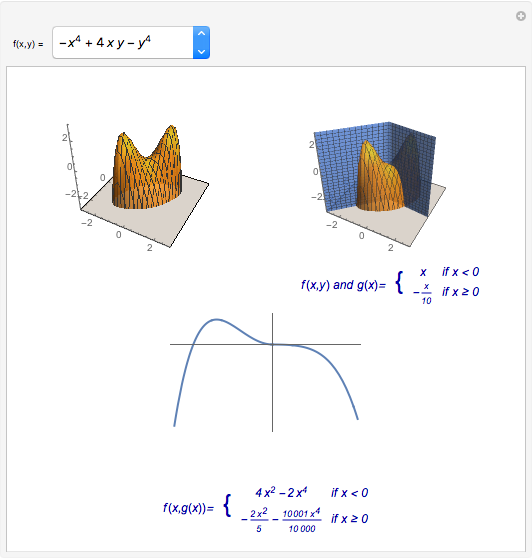
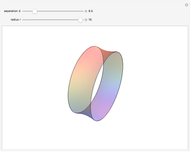
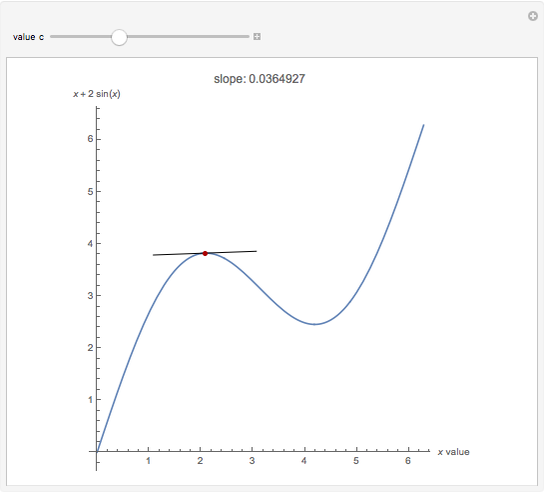
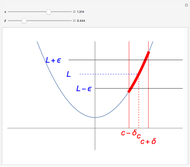
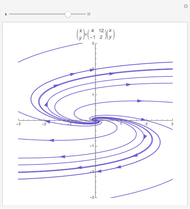
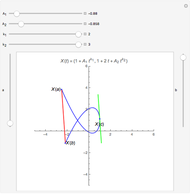
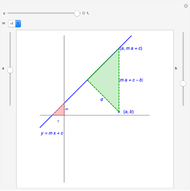
Theorem: Let  be a function with continuous second partial derivatives in a open set
be a function with continuous second partial derivatives in a open set 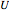 in the plane and let
in the plane and let 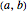 be a saddle point in
be a saddle point in 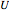 . Then there exists a continuous function
. Then there exists a continuous function  with
with  for which the projection on the
for which the projection on the  plane of the intersection of the surface
plane of the intersection of the surface 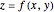 and the cylindrical surface
and the cylindrical surface  has a inflection point at
has a inflection point at  .
.
Contributed by: Soledad Mª Sáez Martínez and Félix Martínez de la Rosa (March 2011)
Open content licensed under CC BY-NC-SA
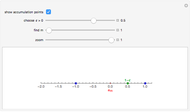
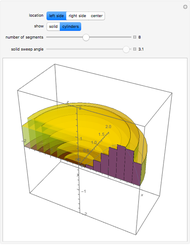
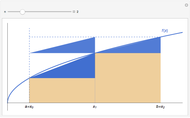
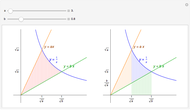
Snapshots
Details
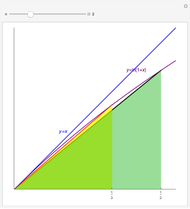
Take the quadratic form  . For each
. For each  and
and 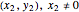 such that
such that 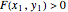 and
and  , the function
, the function  verifies the theorem.
verifies the theorem.
Reference: F. Martínez de la Rosa, "Saddle Points and Inflection Points," The College Mathematics Journal, 38(5), 2007 pp. 380–383.
Permanent Citation