Scalar Feynman Diagrams and Symanzik Polynomials

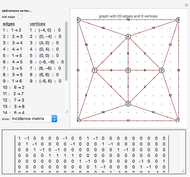
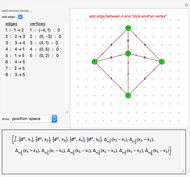
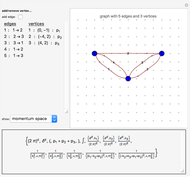
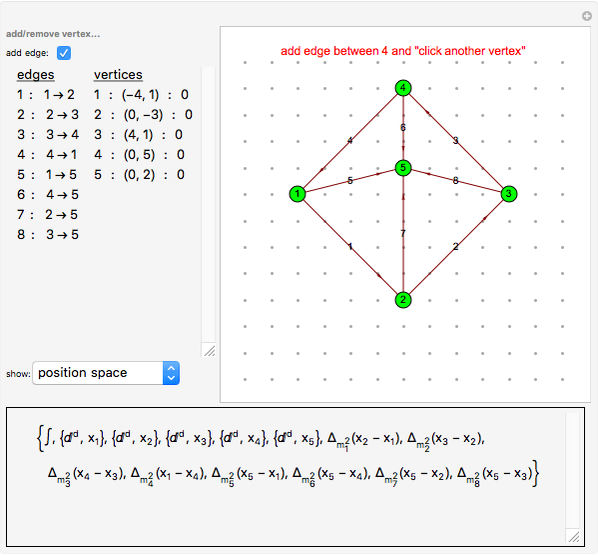
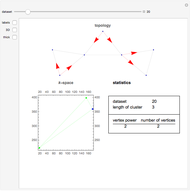
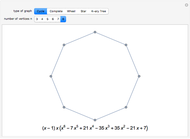
This Demonstration allows the construction of an arbitrary Feynman graph and displays its position space, momentum space, or parametrized amplitude. It assumes a Euclidean, scalar quantum field theory in dimensions and that each propagator 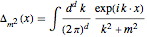can have a different mass. Much of the Demonstration works for arbitrary graphs, but the most interesting are those that are connected and one-particle irreducible.

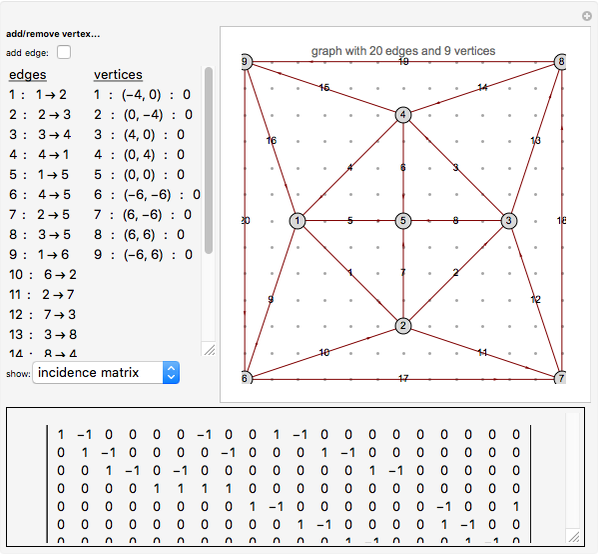
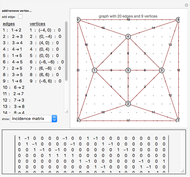
External propagators are not drawn in the graph; rather, vertices are flagged if they have incoming external momentum. The total external momentum is assumed to be conserved. Vertices are added and deleted by command-clicking in the vertex pane; they can be moved by clicking and dragging. Edges are added by activating the appropriate toggle, then clicking the two vertices to be joined. All other changes to the edges and vertices can be made in the popup menus of the left-hand panel. Information about the Feynman graphs selected in the lower left-hand menu and is displayed in the bottom pane. All graph data is printable from the supplied menus for use in other programs and calculations. Most objects in the Demonstration have tooltips describing their use.

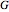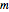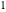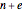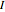Consider a graph with edges, vertices, and external edges connected to external vertices; the assumption that external vertices have only one external edge affects only the expression for the position-space amplitude but is easily remedied. Index the edges from to , where the final are the external edges. Similarly index the vertices. If we introduce the incidence matrix , then the Feynman amplitude associated with the graph is

.

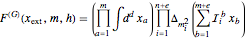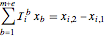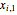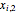Note that , where and are the beginning and ending points of the edge indexed by .

Taking the Fourier transform and truncating the external propagators gives the corresponding momentum space amplitude

.

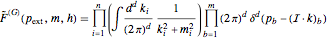The external momenta 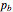are always considered as incoming and are associated with the external edge that is connected to the vertex at 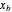. The -functions combine to give conservation of total external momentum (a factor of 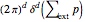) and the rest can be integrated leaving (for a connected graph) 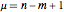momentum integrals; is the number of independent loops in the graph.

The momentum space amplitude can then be written in either Feynman parameters

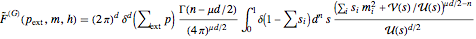
or Schwinger parameters (also known as proper-time or -parameters)

,

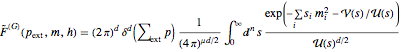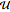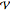where and are the Symanzik polynomials. The first Symanzik polynomial (also known as the Kirchhoff–Symanzik polynomial) is homogeneous in 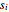of order and can be written as a sum-product over the trees of the graph: 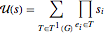, where the 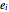denote the edges. The second Symanzik polynomial is a quadratic form in the external momenta 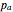and is homogeneous in 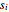of order 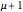. It can be expanded over the two-trees (two-component spanning forests) of the graph: 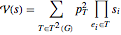, where 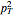is the total momentum squared flowing into either of the connected components of the two-tree. Total momentum conservation means that it does not matter which component is chosen.

Some good references are

N. Nakanishi, Graph Theory and Feynman Integrals, Newark, NJ: Gordon and Breach, 1971.

V. A. Smirnov, Evaluating Feynman integrals, New York: Springer, 2004.

C. Itzykson and J.–B. Zuber, Quantum Field Theory, New York: McGraw–Hill, 1980.