Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

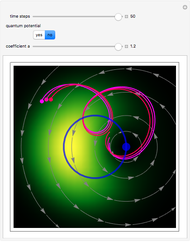
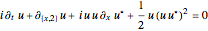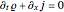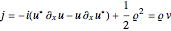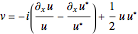Bohm Trajectories for a Type of Derivative Nonlinear Schrödinger Equation

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

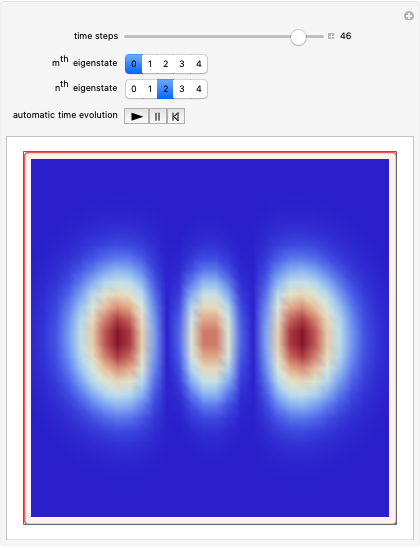
The time-evolution of the quantum standard wavefunction is determined by the Schrödinger equation and guidance equation. The guidance equation states that the velocity field for the configuration is given by the quantum current 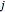divided by the density . The guidance equation is derived from the continuity equation, which is a special form of a conservation law.

[more]

The velocity field as given for the Schrödinger equation cannot be applied in general. For some nonlinear Schrödinger equations, an acceptable velocity field must be derived from the continuity equation with a modified current. The new velocity field is then postulated to equal the current divided by the density.

Such an example is presented here. In this Demonstration the current is derived from a type of Derivative Nonlinear Schrödinger Equation (DNLSE). The DNLSE is defined by , where is a complex function that depends on , and and is the complex conjugate.

The modified current is obtained from the continuity equation , where the current with the density . For the DNLSE case, the velocity must be changed to to satisfy the continuity equation. The guidance equation (here with =0.5 and =1) was developed by de Broglie in the 1920s for the Schrödinger equation and was first introduced at the famous Solvay conference in 1927. The resulting dynamics from the guidance equation were called "pilot wave theory" by de Broglie. The pilot wave theory was rediscovered by David Bohm in 1952.

[less]

Contributed by: Klaus von Bloh (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

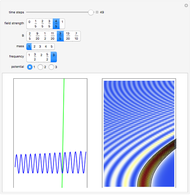
The Hirota bilinear method is applied to find exact -soliton solutions for the DNLSE (see references). For this Demonstration a two-soliton solution is taken. The soliton has four free real parameters (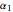, , 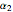, 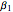) that characterize the velocity, the amplitude, and the width of the 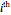soliton. Due to the limited CPU power, only is chosen as a free parameter. The other parameters can be found in the para options in the program. The system is time-reversible.

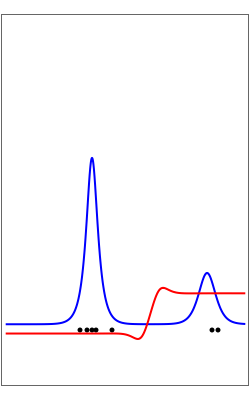
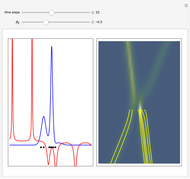
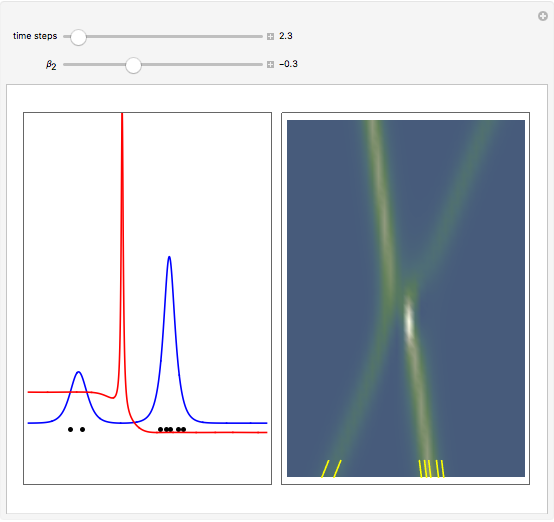
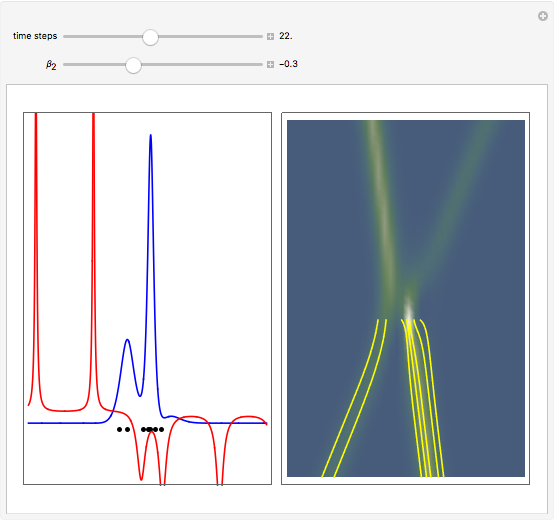
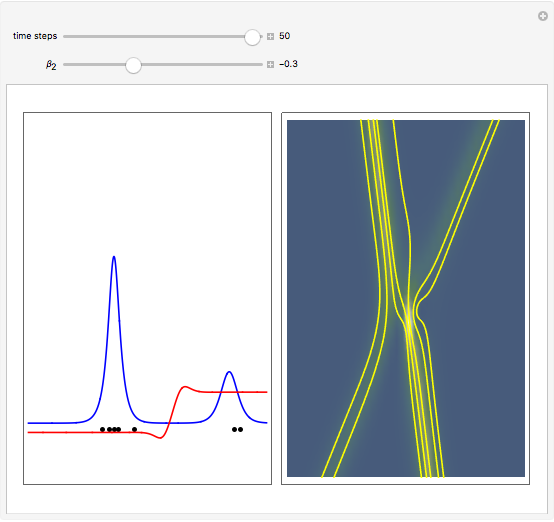
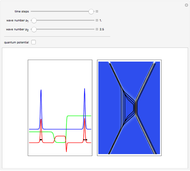
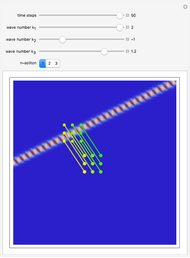
The left graphic shows the position of the particles, the wave amplitude (blue), and the velocity (red). The right graphic shows the wave amplitude and the complete trajectories in (, ) space. The velocity is scaled to fit. In the program, if AccuracyGoal, PrecisionGoal, and MaxSteps are increased, the results will be more accurate.

References:

J. Lee, Y. Lee, and C. Lin, "Exact Solutions of DNLS and Derivative Reaction-Diffusion Systems," Journal of Nonlinear Mathematical Physics, 9(1), 2002 pp. 87–97.

W. Struyve and A. Valentini, "De Broglie-Bohm Guidance Equations for Arbitrary Hamiltonians," ArXiv:quant-ph/0808.0290v2, 2008 pp. 1–22.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send