Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Semigraceful Eulerian Graphs

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

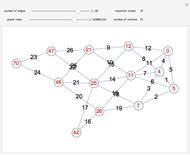
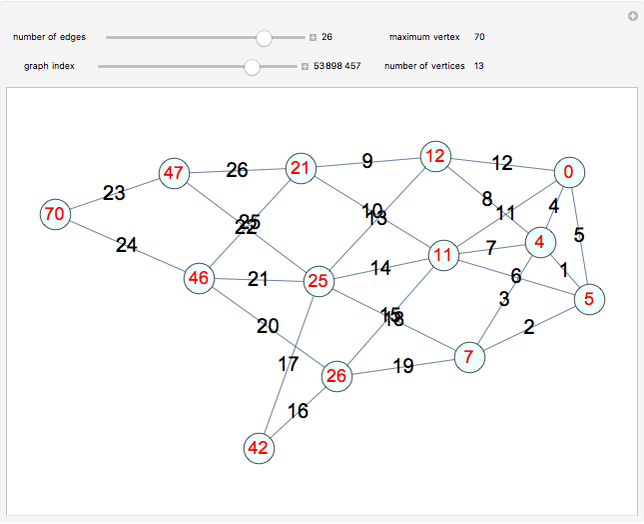
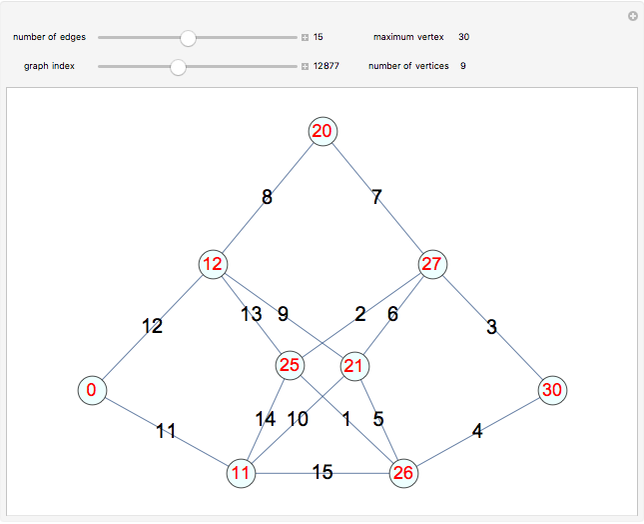
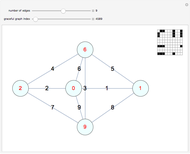
An Eulerian path visits all the edges of a graph in sequence, with no edges repeated. In 1736, Euler solved the Königsberg bridges problem by noting that the four regions of Königsberg each bordered an odd number of bridges, but that only two odd-valenced vertices could be in an Eulerian graph.

[more]

A semigraceful graph has edges labeled 1 to , with each edge label equal to the absolute difference between the labels of its vertices; the lowest vertex label is 0. For a fully graceful graph, the highest vertex label is .

This Demonstration looks at Eulerian semigraceful graphs. When the maximal vertex equals the number of edges, the graph is fully graceful.

[less]

Contributed by: Ed Pegg Jr (August 2015)
Open content licensed under CC BY-NC-SA

Snapshots

Details

detailSectionParagraph
Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send