Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

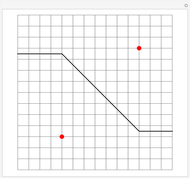
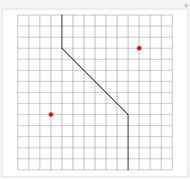
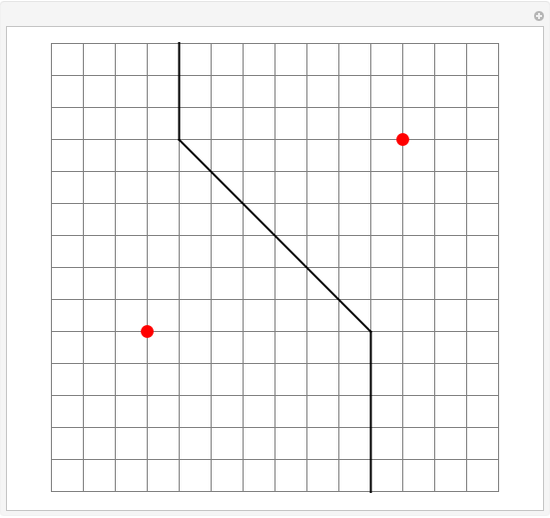
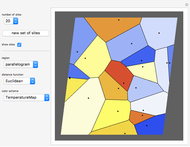
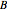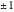Set of Points Equidistant from Two Points in Taxicab Geometry

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

In taxicab geometry, the usual Euclidean distance between points is replaced by the sum of the absolute differences of their coordinates. In symbols, if the two points are 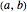and 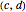, the distance between them is 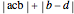. The taxicab distance is also called Manhattan distance or rectilinear distance.

[more]

Drag the two red points (discretized only to help in checking) to see the set of points equidistant to them, which forms the "bisector line" of the segment joining the points. If the two points are different, there are three possibilities for this "line":

1. When the line through the points has slope 0 or ∞, coincides with the usual Euclidean bisector line.

2. When the line through the points has slope , takes the shape of two infinite square regions (colored in blue) joined by a line segment.

3. Otherwise, forms a zigzag line.

[less]

Contributed by: Jaime Rangel-Mondragon (July 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send