Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Side Capacity Model of Stagnancy in a Continuous Stirred-Tank Reactor

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

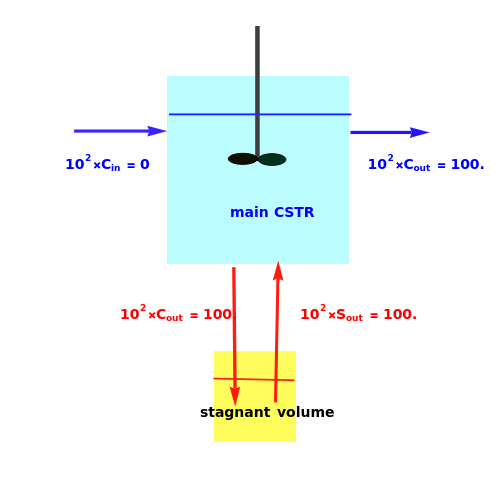
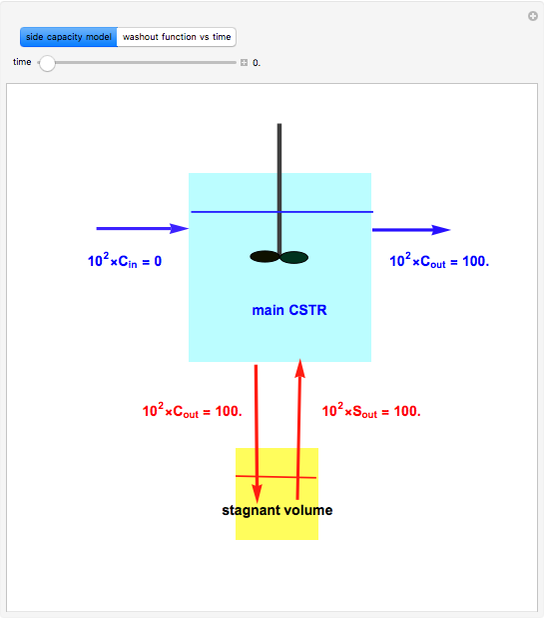
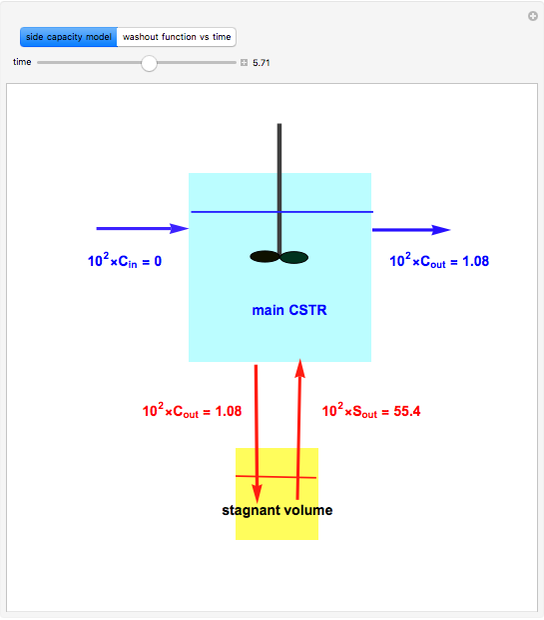
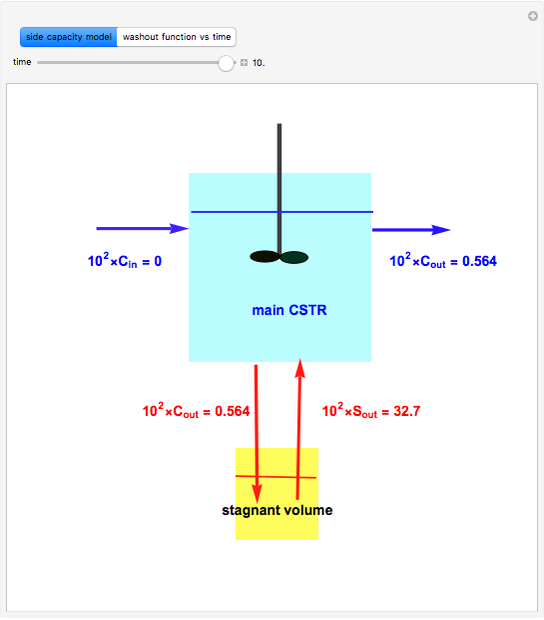
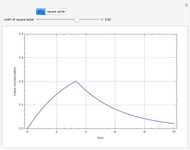
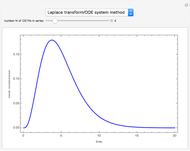
A Continuous Stirred-Tank Reactor (CSTR) has a well-mixed volume (main CSTR) of 7 , and a stagnant volume of 1 . Stagnancy behavior is taken into account using the side-capacity model. Flow rates in the main CSTR and the stagnant volume are 8 and 0.125, respectively (both expressed in 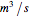). In a washout experiment, the reactor is initially filled with a tracer (e.g. . Then the inlet concentration of tracer versus time is set equal to zero. As expected, the concentration of the tracer in the reactor will tend to zero, because the tracer starts leaving the reactor at .

[more]

This Demonstration shows the washout function (i.e., the tracer concentration exiting the main CSTR) versus time. This function has to be plotted on a log-scale in order to clearly see the two distinct residence times (one for the main CSTR and the other for the stagnant volume). Indeed, two regions, which exhibit linear behavior with different slopes, are observed. The blue dashed slope corresponds to the residence time in the main CSTR while the green dashed slope represents the residence time in the stagnant volume. Finally, a schematic figure shows the side-capacity model as well as the exit concentrations from the main CSTR and the stagnant volume at user-specified values of time.

[less]

Contributed by: Housam Binous (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

E. B. Nauman, Chemical Reactor Design, Optimization, and Scaleup, 2nd. ed., Hoboken, NJ: Wiley, 2008.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send