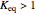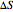Simplified Statistical Model for Equilibrium Constant

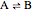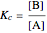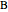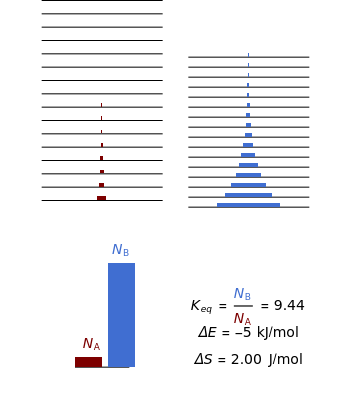
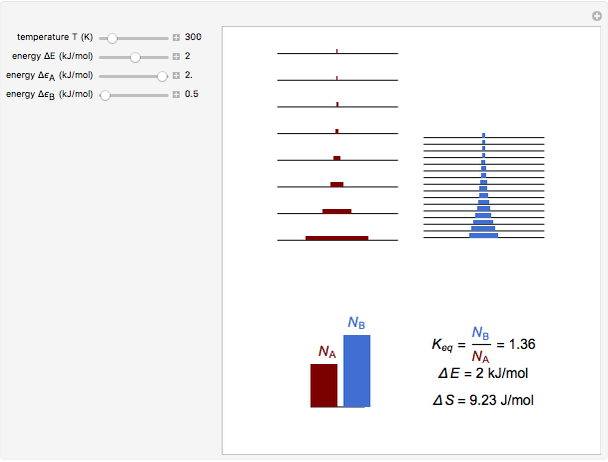
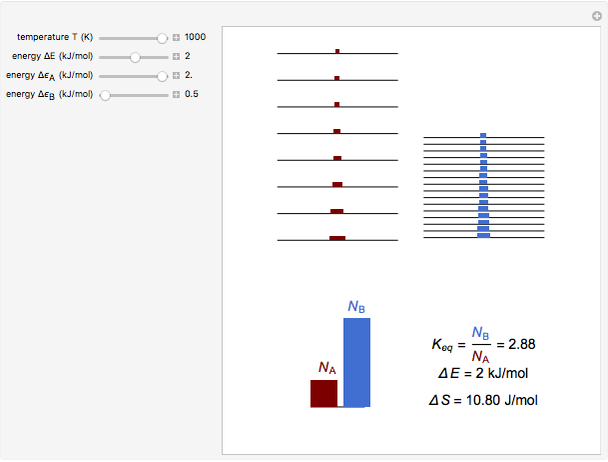
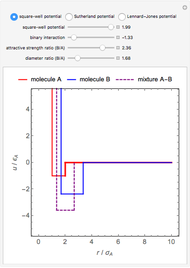
Consider a simple chemical equilibrium with equilibrium constant . (This can alternatively be written in terms of the concentrations of and .) The difference in electronic energy for the reaction equals 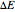, conveniently expressed in kJ/mol. Let the internal structure of each molecule be idealized as a series of equally spaced energy levels (similar to those of a harmonic oscillator), with the energy increments and 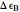. The spacings and 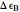relative to 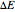are exaggerated in the graphic for easier visualization. The sublevels of each molecular species are assumed to occupy a Boltzmann distribution at temperature . Accordingly, , where , the molecular partition function for , and analogously for 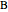. For a mixture of and 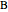, a single Boltzmann distribution can be considered to apply for the composite levels of both molecules. This leads to the formula for equilibrium constant in statistical thermodynamics: .

Under constant volume conditions, the equilibrium constant is related to the change in Helmholtz free energy: . An exothermic reaction, with , tends to give , implying that the forward reaction is favored. This can be reversed, however, with the endothermic reaction favored if the entropy change is sufficiently negative. This could result if species has a greater number of thermally accessible levels at the given temperature.