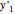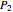Smirnoff's Graphic Solution of a Second-Order Differential Equation
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
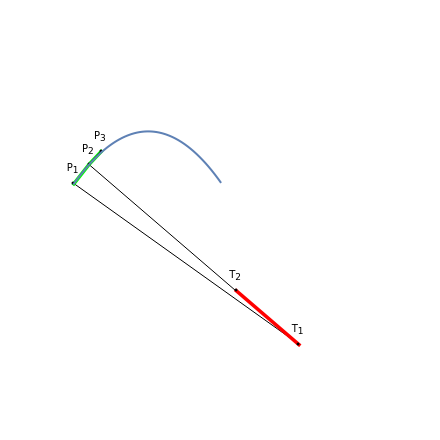
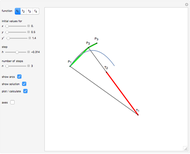
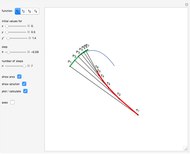
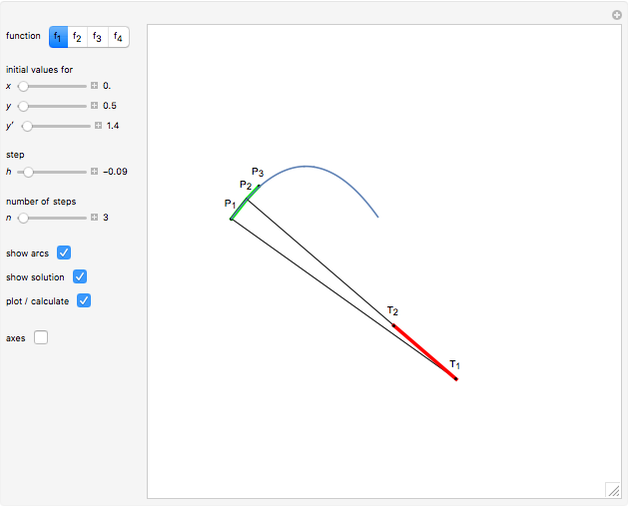
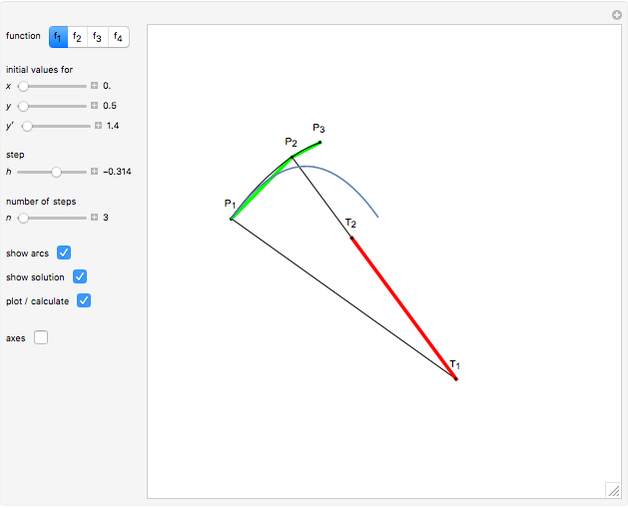
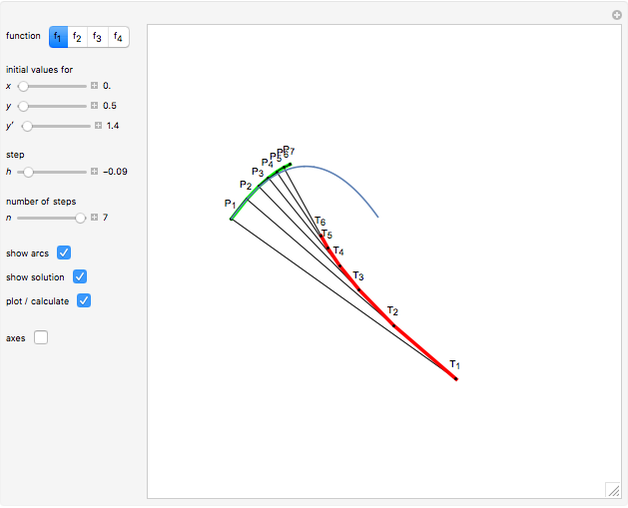
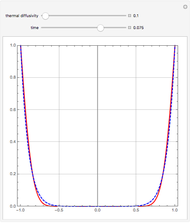
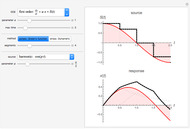
This Demonstration shows a method of graphically approximating solutions of second-order differential equations. Let  be a given differential equation,
be a given differential equation,  be the arc length of an integral curve, and
be the arc length of an integral curve, and  the angle between the tangent and the
the angle between the tangent and the  axis. Therefore
axis. Therefore  ,
,  . Differentiate the first equation to get
. Differentiate the first equation to get 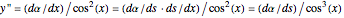 .
.
Contributed by: Izidor Hafner (February 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] V. I. Smirnoff, Lectures in Higher Mathematics, Vol. 2, Moscow: Nauka, 1967 pp. 48–50.
Permanent Citation