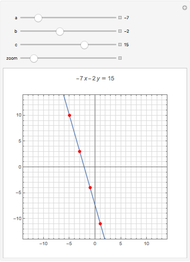
Solving a Linear Diophantine Equation in Two Variables by the Euclidean Algorithm

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
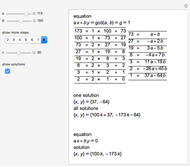
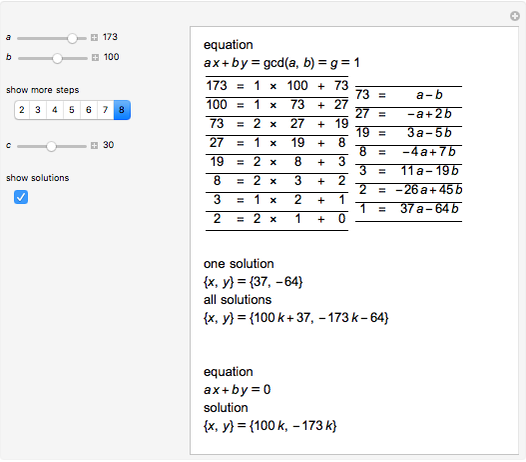
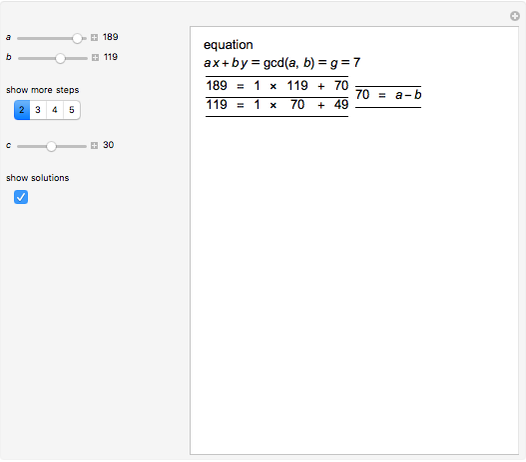
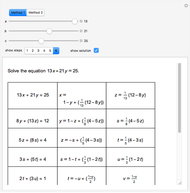
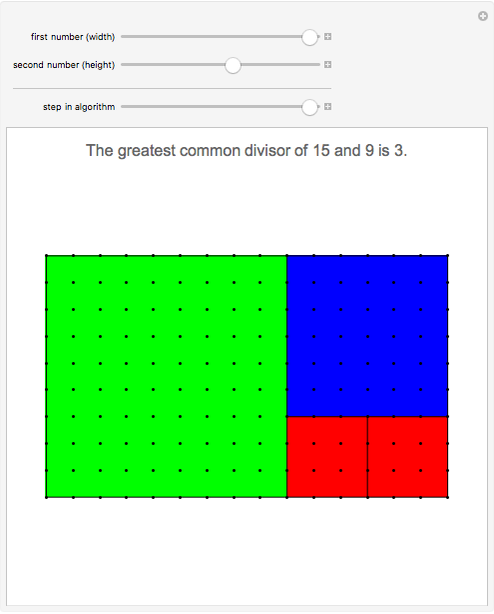
This Demonstration shows the solutions of Diophantine equations of the form 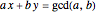 ,
, 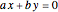 and
and 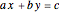 using the Euclidean algorithm.
using the Euclidean algorithm.
Contributed by: Izidor Hafner (September 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A linear Diophantine equation can have either no solutions, exactly one solution or infinitely many solutions.
Let  and
and  be nonzero integers, and let
be nonzero integers, and let 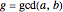 . The equation
. The equation 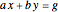 always has a solution
always has a solution  in integers, and this solution can be found by the Euclidean algorithm. Then every solution to the equation can be obtained by substituting for the integer
in integers, and this solution can be found by the Euclidean algorithm. Then every solution to the equation can be obtained by substituting for the integer  in the formula
in the formula
 [1, p. 37].
[1, p. 37].
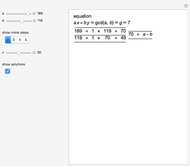
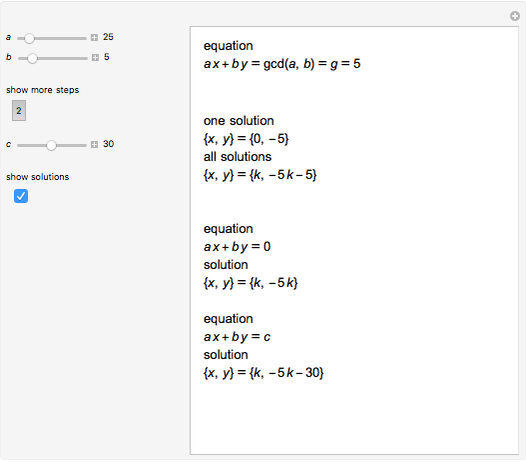
If 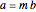 , then we have the equation
, then we have the equation 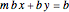 , which is
, which is  . It has one solution
. It has one solution  , and the general solution is
, and the general solution is 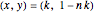 .
.
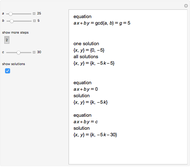
The homogeneous equation 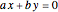 has the general solution
has the general solution  .
.
The Diophantine equation 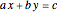 has no solution if
has no solution if  if not divisible by
if not divisible by  . If
. If 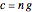 , then the equation has the general solution
, then the equation has the general solution  , so that
, so that 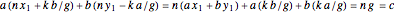 .
.

[1]. J. H. Silverman, A Friendly Introduction to Number Theory, Upper Saddle River, NJ: Prentice Hall, 1997.
Permanent Citation