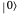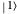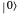Stern-Gerlach Simulations on a Quantum Computer

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
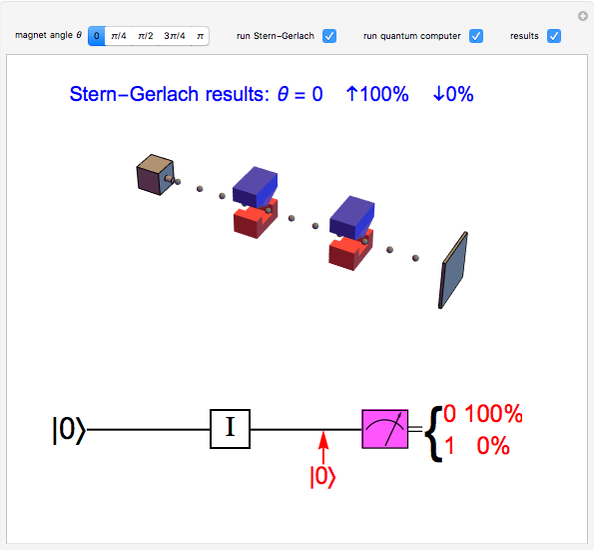
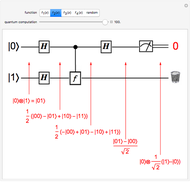
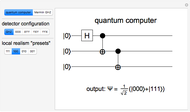
In the Stern–Gerlach experiment, an unpolarized beam of neutral particles of spin 1/2 is directed through an inhomogeneous magnetic field (blue and red magnet), which produces separated beams of spin-up and spin-down particles. For simplicity, only the outgoing spin-up beam is shown in the graphic. This beam is then directed through a second magnet, for which the polarization can be rotated by an angle  from the original. This further splits the beam (except when
from the original. This further splits the beam (except when  or
or  ) into spin-up and spin-down beams with respect to the new polarization direction. Again, only the spin-up component is shown. The probability for a particle to emerge with spin-up (↑) or spin-down (↓) is given by
) into spin-up and spin-down beams with respect to the new polarization direction. Again, only the spin-up component is shown. The probability for a particle to emerge with spin-up (↑) or spin-down (↓) is given by 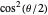 and
and 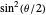 , respectively. The resulting probabilities of ↑ and ↓ are shown for five selected angles.
, respectively. The resulting probabilities of ↑ and ↓ are shown for five selected angles.
Contributed by: S. M. Blinder (June 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
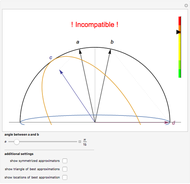
The action of the single-qubit quantum gates can be represented by  unitary matrices acting on the qubit
unitary matrices acting on the qubit 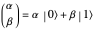 :
:
identity (or IDLE):  ,
,
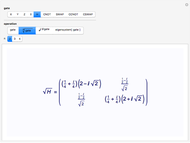
Hadamard gate:  ,
,
Pauli X (or NOT) gate: 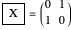 ,
,
phase (or 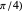 gate:
gate: 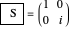 ,
,
 gate:
gate: 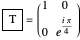 .
.
For example, the 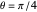 rotation is produced by the sequence
rotation is produced by the sequence
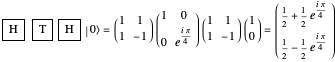 .
.
The probability of a result 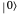 in the subsequent measurement is then given by
in the subsequent measurement is then given by
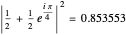 , or about 85% spin-up.
, or about 85% spin-up.
References
[1] Wikipedia. "Stern–Gerlach Experiment." (Jun 9, 2017) en.wikipedia.org/wiki/Stern-Gerlach_experiment.
[2] M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition, Cambridge: Cambridge University Press, 2010. doi:10.1017/CBO9780511976667.
[3] G. Fano and S. M. Blinder, Twenty-First Century Quantum Mechanics: Hilbert Space to Quantum Computers, New York: Springer Berlin Heidelberg, 2017.
Permanent Citation