Taylor Expansions with Noninteger Number of Terms

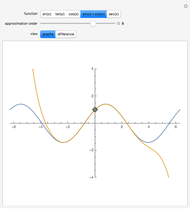
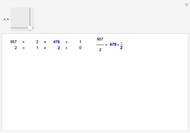
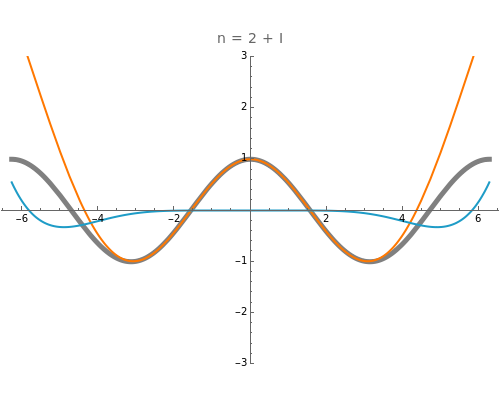
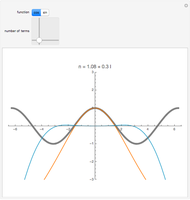
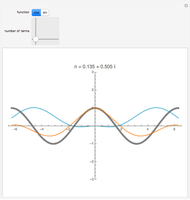
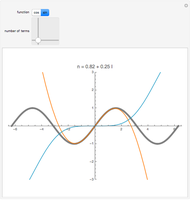
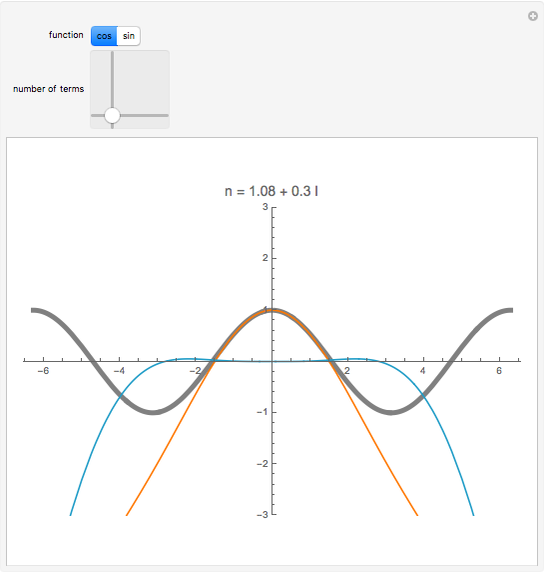
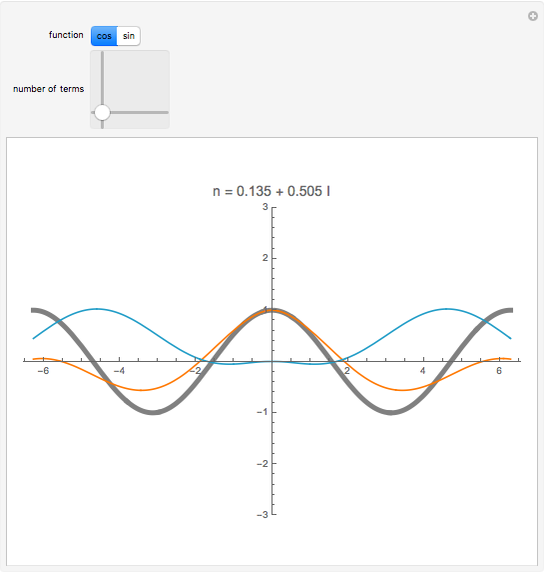
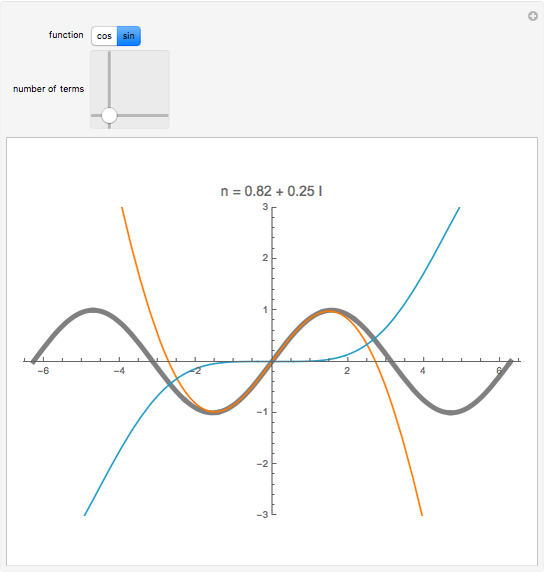
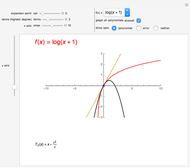
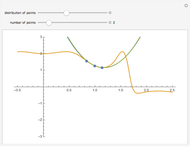
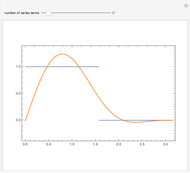
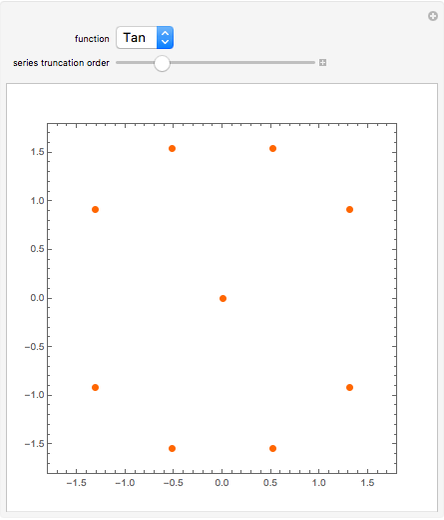
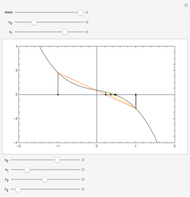
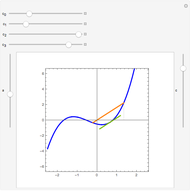
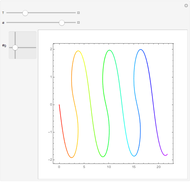
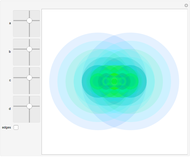
At regular points , an analytic function can be expanded in a series of the form . In case it is possible to obtain a closed form of the truncated series as an analytic function of , we can consider this to be a natural continuation of the Taylor series to an noninteger (even complex) number of terms. This Demonstration plots these continuations for the functions cosine and sine. The gray curve is the original function; the orange and blue curves are the real and imaginary parts of the analytic continuation.