Fitness Model for Gene Frequency in Populations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
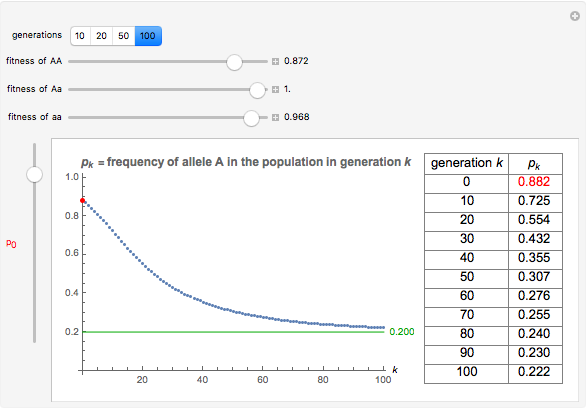
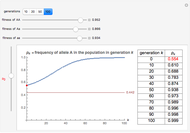
Imagine a single gene with two alleles, A and a, where the frequency of the A allele in the gene pool of an entire population is 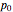 . Assuming that this is a large and isolated population, that there is random mating, and that there are fixed fitness coefficients for each of the three possible genotypes AA, Aa, and aa through the generations, one can predict the frequency
. Assuming that this is a large and isolated population, that there is random mating, and that there are fixed fitness coefficients for each of the three possible genotypes AA, Aa, and aa through the generations, one can predict the frequency 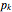 of the A allele in the population after
of the A allele in the population after  generations.
generations.
Contributed by: Bruce Torrence (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
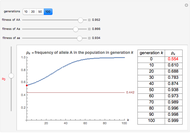
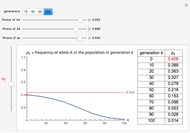
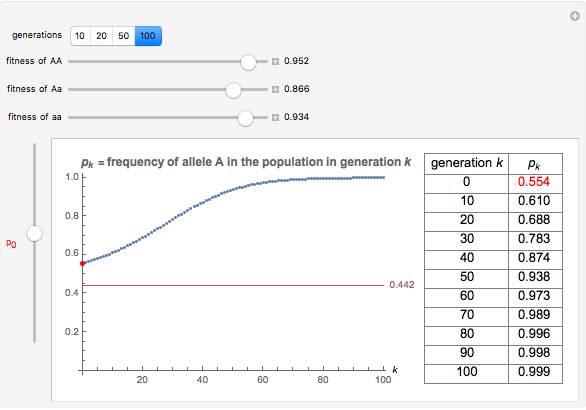
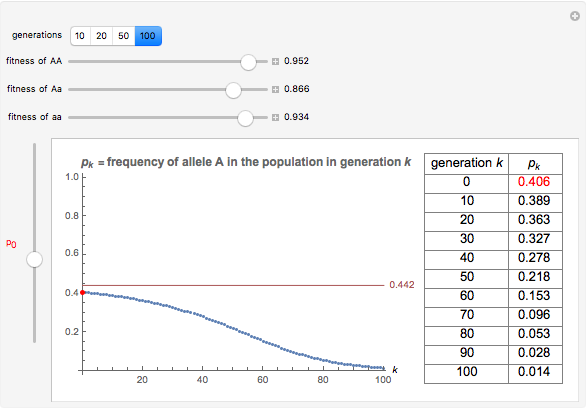
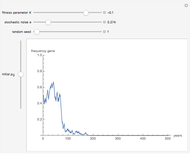
You will find that in some cases the A allele will truly become dominant and the other allele will go extinct (e.g., see Snapshot 1). Even with the same fitness coefficients, if the initial allele frequency of A is sufficiently small, it will go extinct (Snapshot 2). And in the case of heterozygous advantage (when the Aa fitness coefficient is 100% and the others are less), a stable limiting value for the frequency of A will manifest itself (Snapshot 3). This limiting value is indicated by a green line. The most famous example of heterozygous advantage is that of sickle cell anemia in certain tropical populations.
In some other cases a red horizontal line appears. This is a repelling (rather than attracting) stable value for the allele frequencies. That is, if 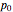 is less than this value,
is less than this value, 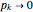 , while if
, while if 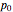 is greater than this value,
is greater than this value, 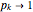 . Whether red or green, the limiting value is given by
. Whether red or green, the limiting value is given by 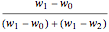 , where
, where 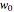 ,
, 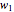 , and
, and 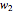 are the fitness coefficients for aa, Aa, and AA, respectively.
are the fitness coefficients for aa, Aa, and AA, respectively.
The mathematics behind this Demonstration is quite simple and is widely documented. See, for example, chapter 6.4 of E. S. Allman and J. A. Rhodes, Mathematical Models in Biology: An Introduction, New York: Cambridge University Press, 2004.
Permanent Citation