Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Running in the Rain

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

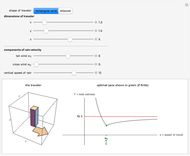
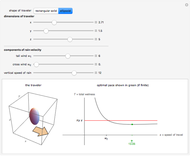
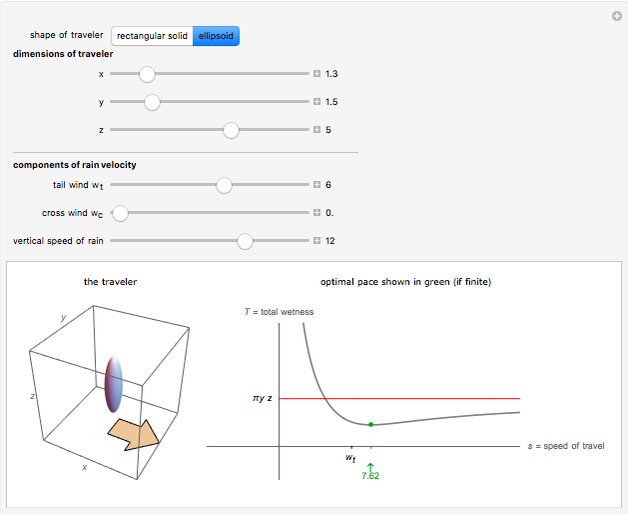
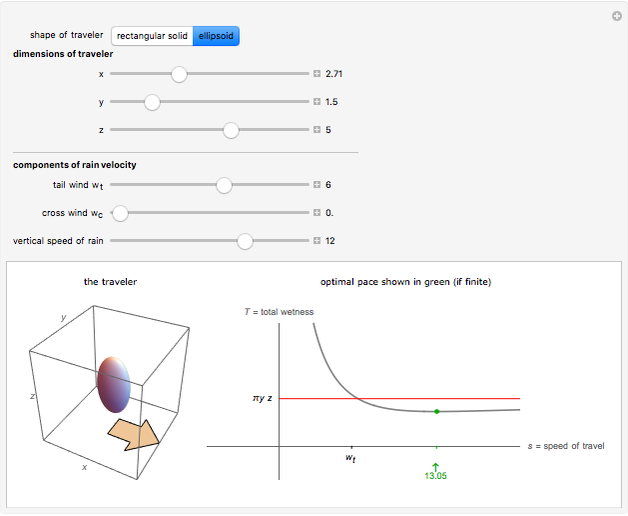
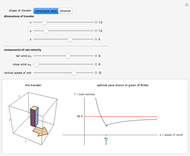
To stay driest, is it better to walk or run in the rain? The conventional wisdom was conveyed in a limerick by Matthew Wright in New Scientist magazine in 1995: "When caught in the rain without mac, walk as fast as the wind at your back. But when the wind's in your face, the optimal pace is as fast as your legs will make track." But this advice is only partially correct. Yes, in the absence of a tail-wind, running flat out is best. But "as fast as the wind at your back" is misleading. It is the best pace for box-shaped travelers provided the tail-wind is sufficiently strong. But if the tail-wind is too weak, or if you are a more well-rounded individual (in appearance, at least), then your optimal pace exceeds that of the tail wind.

[more]

This Demonstration calculates total wetness for box-shaped and ellipsoidal travelers moving in a straight line in prescribed rain conditions. The wetness measure is simply the volume of the rain region, the region in space containing all the drops that will strike the traveler as he moves a distance of one unit in the positive direction (his direction of travel is indicated by the large arrow in the left frame). Total wetness is graphed in the right panel as a function of the traveler's speed, and the optimal speed of travel is shown in green provided that it is finite.

It is interesting to note that for ellipsoidal travelers, the optimal pace is very sensitive to changes in the dimension of the traveler. Chubby travelers seem better served by running faster. For rectangular travelers, minor perturbations in the dimension make no difference whatever.

[less]

Contributed by: Bruce Torrence (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

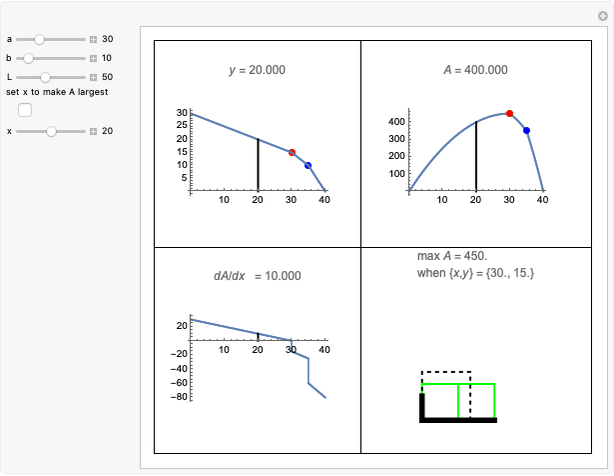
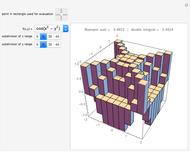
The "dimensions of traveler" controls set the lengths of the semi-axes of an ellipsoidal traveler, and half the lengths of the sides of a rectangular-solid traveler. The area of the front face of a rectangular-solid traveler is therefore , while the corresponding projection for an ellipsoidal traveler is . If the traveler moves one unit forward at super-speed, the rain region approaches a horizontal cylinder whose volume approaches these values. Hence total wetness is asymptotic to the red line shown.

Complete derivations of the wetness functions can be found here:

D. Kalman and B. Torrence, "Keeping Dry: The Mathematics of Running in the Rain," Mathematics Magazine, 82(4), 2009.

Wright's limerick was first published here:

M. Wright, "Letter to the Editor," New Scientist, 1960, 1995 p. 57.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send