The Seven Crystal Classes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
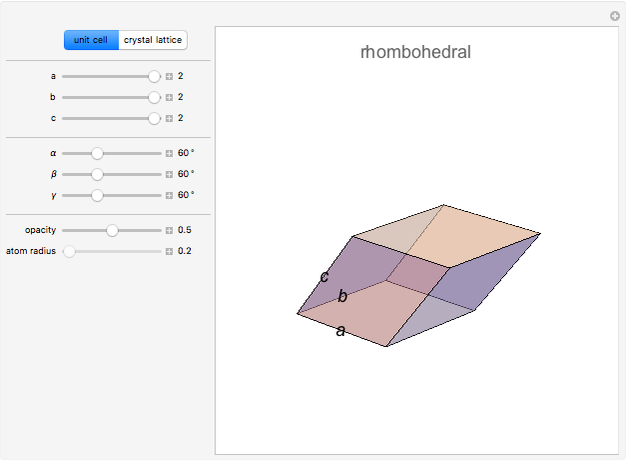
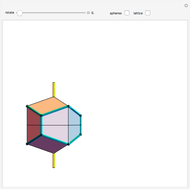
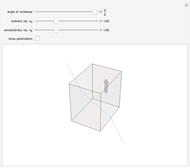
The three-dimensional arrangement of the atoms, molecules, or ions in a crystalline solid can be described by the geometry of its unit cell. The entire crystal can then be constructed by translational repetitions of the unit cell. A unit cell is described by six lattice parameters: edge dimensions  ,
,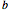 ,
,  and inter-edge angles
and inter-edge angles  ,
, 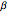 ,
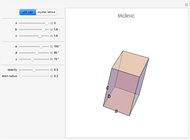
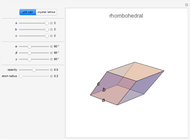
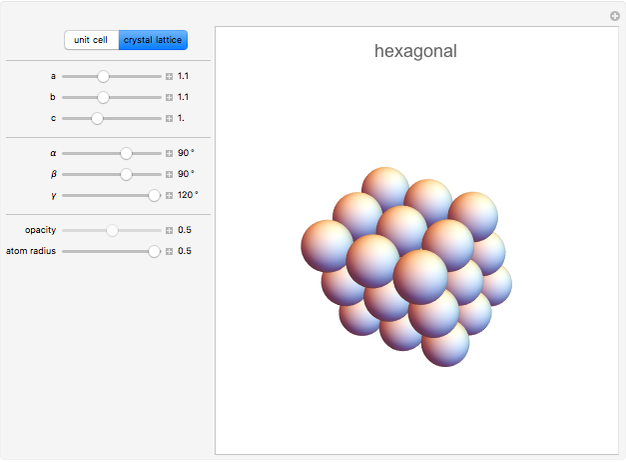
,  . There are seven possible crystal systems that can produce an infinite lattice in three-dimensional space so that each lattice point has an identical environment. Depending on relationships between lattice parameters, the seven crystal systems are classified as cubic (or isometric), tetragonal, orthorhombic, rhombohedral (or trigonal), hexagonal, monoclinic, and triclinic. (This Demonstration does not consider further classifications within these crystal systems, such as body-centered, face-centered, etc., which make up a total of 14 Bravais lattices.)
. There are seven possible crystal systems that can produce an infinite lattice in three-dimensional space so that each lattice point has an identical environment. Depending on relationships between lattice parameters, the seven crystal systems are classified as cubic (or isometric), tetragonal, orthorhombic, rhombohedral (or trigonal), hexagonal, monoclinic, and triclinic. (This Demonstration does not consider further classifications within these crystal systems, such as body-centered, face-centered, etc., which make up a total of 14 Bravais lattices.)
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: unit cell of triclinic class, the lowest symmetry type
Snapshot 2: rhombohedral unit cell
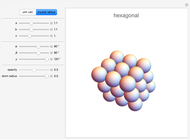
Snapshot 3: Hexagonal closest packing (HCP) of spheres, filling about 74% of three-dimensional space. Cubic closest packing (CCP) using a face-centered lattice (not available in this Demonstration) fills an equal fraction of space. Kepler conjectured that these are the densest possible arrangements of spheres. (A proof by Thomas Hales in 1998 is considered "99% certain".)
Permanent Citation