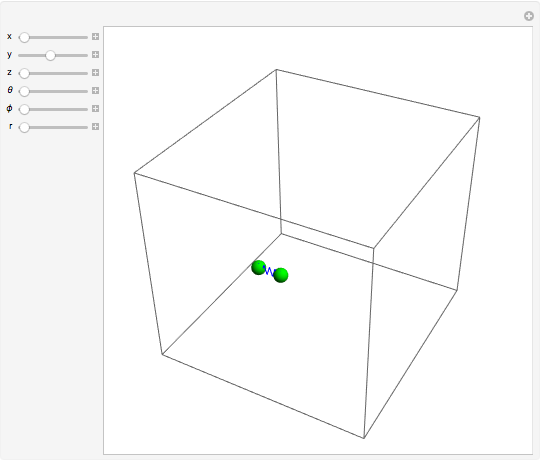
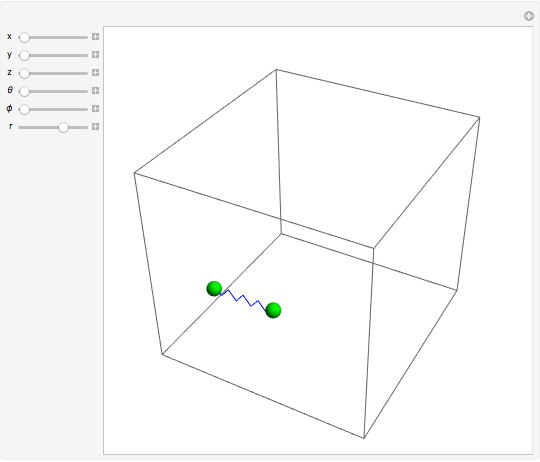
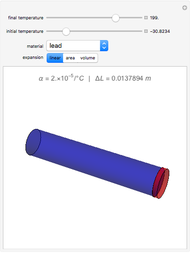
The Six Degrees of Freedom of a Diatomic Molecule

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
For a diatomic molecule at sufficiently high temperatures, the equipartition of energy theorem distributes an equal portion of the energy, equal to 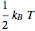 , among each quadratic term in the Hamiltonian. Here
, among each quadratic term in the Hamiltonian. Here 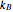 is the Boltzmann constant and
is the Boltzmann constant and  is the absolute temperature. Three of the degrees of freedom are translations, two are rotations, and one is vibration. The vibrational degree of freedom contributes a total energy
is the absolute temperature. Three of the degrees of freedom are translations, two are rotations, and one is vibration. The vibrational degree of freedom contributes a total energy 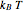 since the associated kinetic energy and potential energy are both quadratic forms. The temperature should not be too high (say,
since the associated kinetic energy and potential energy are both quadratic forms. The temperature should not be too high (say,  K), otherwise electronic degrees of freedom might be excited.
K), otherwise electronic degrees of freedom might be excited.
Contributed by: Enrique Zeleny (August 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For the translations, the kinetic energy is equal to 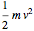 in each direction
in each direction  ,
, 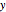 , and
, and  ; for the rotations,
; for the rotations, 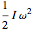 for angles θ and &straightpi;, where
for angles θ and &straightpi;, where 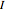 is the moment of inertia of the molecule and
is the moment of inertia of the molecule and  is the angular velocity. Finally, the energy associated with the vibrational degree of freedom, in the harmonic oscillator approximation, can be written as
is the angular velocity. Finally, the energy associated with the vibrational degree of freedom, in the harmonic oscillator approximation, can be written as 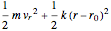 , where
, where 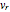 is the velocity along the direction of the chemical bond,
is the velocity along the direction of the chemical bond,  is a spring constant associated with the chemical bond,
is a spring constant associated with the chemical bond,  is the elongation or compression, and
is the elongation or compression, and 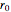 is the equilibrium position. Adding the energies of all six degrees gives a theoretical value for the molar heat capacity at constant volume
is the equilibrium position. Adding the energies of all six degrees gives a theoretical value for the molar heat capacity at constant volume 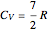 , where
, where 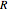 is the universal gas constant.
is the universal gas constant.
Permanent Citation