Boltzmann Gas

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
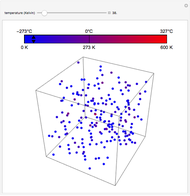
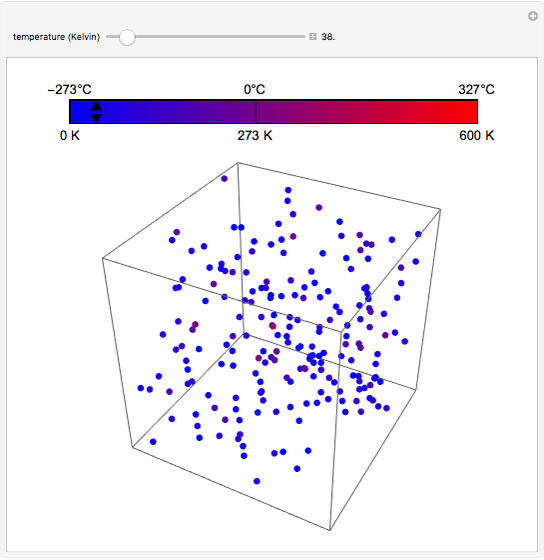
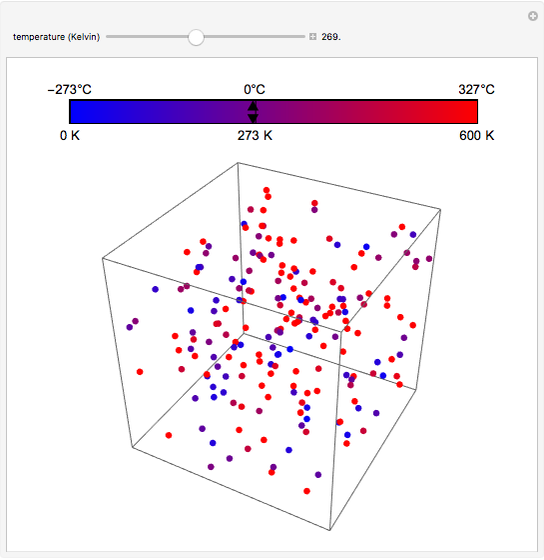
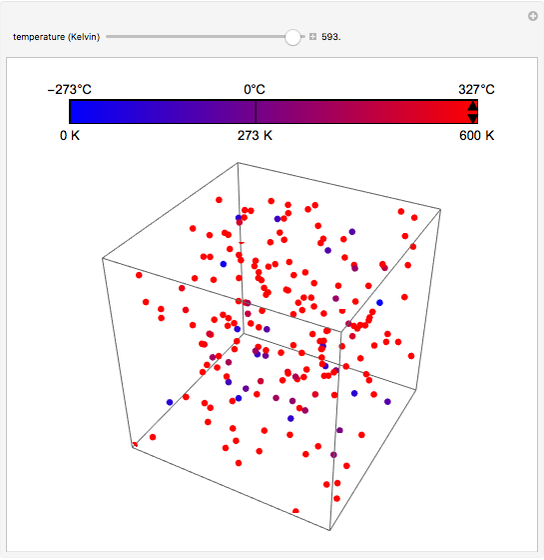
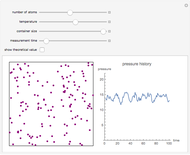
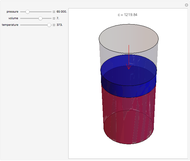
At the macroscopic level, the temperature 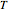 of a substance is a parameter—measured by a thermometer—that indicates how hot or cold the substance is. At the microscopic level, the temperature—according to Ludwig Boltzmann—is a measure of the kinetic energy associated with the disordered motion of the atoms or molecules that constitute the sample. This Demonstration illustrates the relation between atomic motion and temperature in the case of a classical gas (Boltzmann gas) modeled as an ensemble of noninteracting hard spheres. Change the temperature and observe the effect on the motion of atoms or molecules.
of a substance is a parameter—measured by a thermometer—that indicates how hot or cold the substance is. At the microscopic level, the temperature—according to Ludwig Boltzmann—is a measure of the kinetic energy associated with the disordered motion of the atoms or molecules that constitute the sample. This Demonstration illustrates the relation between atomic motion and temperature in the case of a classical gas (Boltzmann gas) modeled as an ensemble of noninteracting hard spheres. Change the temperature and observe the effect on the motion of atoms or molecules.
Contributed by: Gianni Di Domenico (Université de Neuchâtel) and Antoine Weis (Université de Fribourg) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
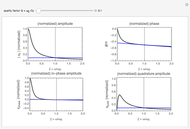
In classical microscopic gas kinetic theory a gas is modeled as an ensemble of hard spheres that do not interact other than by elastic collisions among themselves and with the container walls. If the walls are at a temperature 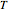 , then the particles' velocity components
, then the particles' velocity components 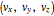 –in the case of thermodynamic equilibrium—obey Maxwell–Boltzmann distributions, for which the probability that a given velocity component,
–in the case of thermodynamic equilibrium—obey Maxwell–Boltzmann distributions, for which the probability that a given velocity component, 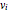 , lies in the interval
, lies in the interval 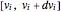 is given by
is given by
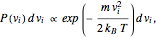
where 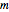 is the mass of the atom and
is the mass of the atom and 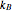 is the Boltzmann constant (see also The Maxwell Speed Distribution). According to the equipartition theorem, the average kinetic energy of each atom is
is the Boltzmann constant (see also The Maxwell Speed Distribution). According to the equipartition theorem, the average kinetic energy of each atom is 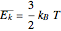 , which shows that, at the microscopic level, the temperature is a direct measure of the energy associated with the disordered atomic motion. The atomic collisions with the container walls are at the origin of the force exerted on the wall that is commonly expressed as the gas pressure (see also Simulation of a Simple Gas Pressure Model). The temperature here is measured in Kelvin (K), and in classical theory all motion comes to a halt at the absolute zero of temperature (
, which shows that, at the microscopic level, the temperature is a direct measure of the energy associated with the disordered atomic motion. The atomic collisions with the container walls are at the origin of the force exerted on the wall that is commonly expressed as the gas pressure (see also Simulation of a Simple Gas Pressure Model). The temperature here is measured in Kelvin (K), and in classical theory all motion comes to a halt at the absolute zero of temperature (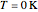 ). The absolute (Kelvin) temperature scale is related to the most commonly used temperature scales of Celsius and Fahrenheit by simple linear relations (see also Temperature Scales and Celsius and Fahrenheit Thermometers).
). The absolute (Kelvin) temperature scale is related to the most commonly used temperature scales of Celsius and Fahrenheit by simple linear relations (see also Temperature Scales and Celsius and Fahrenheit Thermometers).
Permanent Citation