Thermal Degradation of Three Nutrients in Foods

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
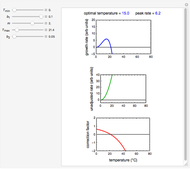
Foods, especially fortified ones, contain several nutrients—for example, vitamins, whose thermal degradation during storage follows different kinetics. This implies that different constant storage temperatures or nonisothermal temperature histories would result in different absolute and relative retention levels at different times. This Demonstration simulates isothermal and nonisothermal degradation curves of three hypothetical nutrients following the same or different kinetic orders. The temperature dependence of their rate constants is assumed to follow an exponential model, which can be used interchangeably with the traditional Arrhenius equation.
Contributed by: Mark D. Normand and Micha Peleg (August 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
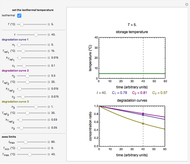
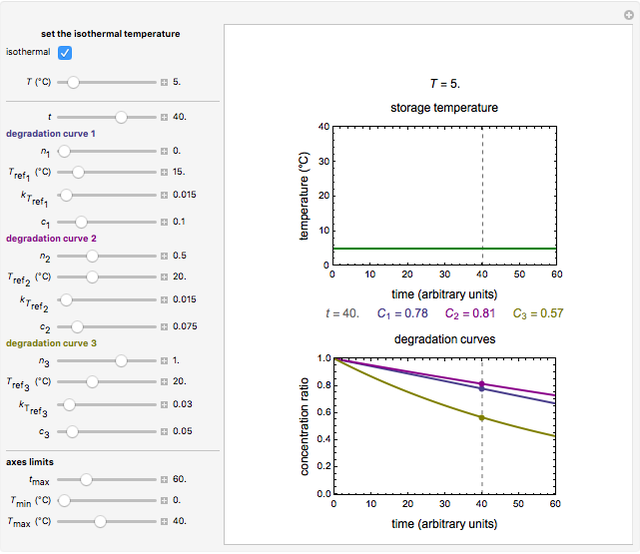
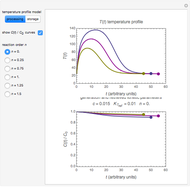
Snapshot 1: isothermal degradation curves of three hypothetical nutrients at 5 °C (refrigeration storage temperature)
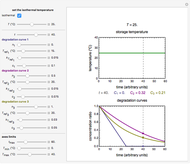
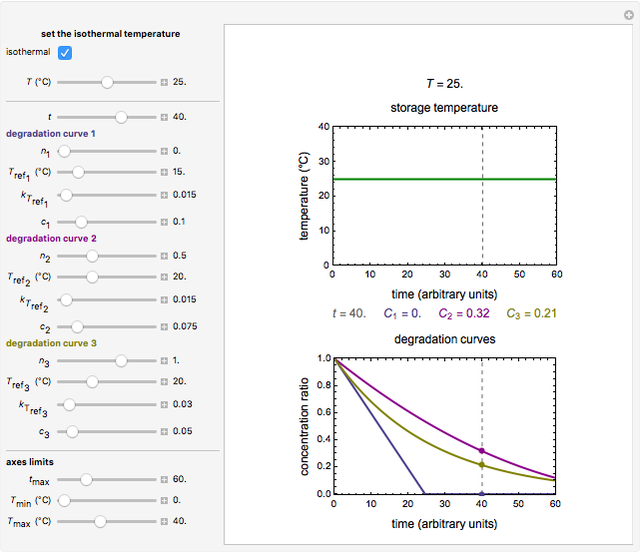
Snapshot 2: isothermal degradation curves of the same three hypothetical nutrients at 25 °C (ambient temperature)
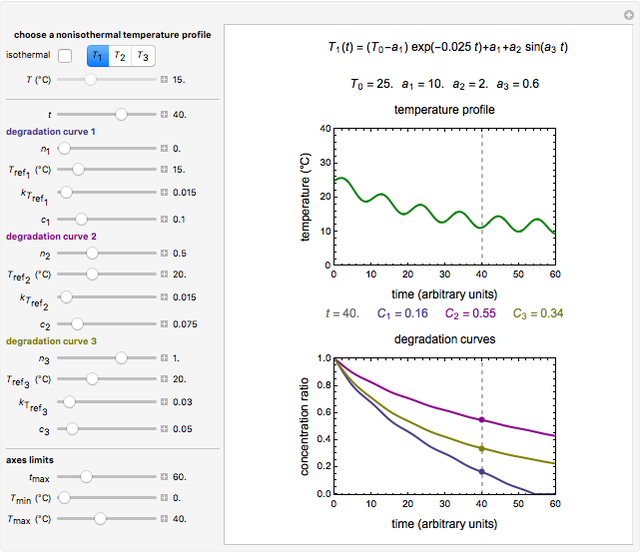
Snapshot 3: nonisothermal degradation curves of three hypothetical nutrients under oscillating falling ambient temperature
Snapshot 4: nonisothermal degradation curves of the same three hypothetical nutrients under oscillating and rising temperature
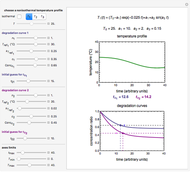
The degradation of many vitamins follows fixed-order kinetics—that is, the rate equation 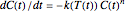 , where
, where 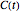 is the concentration in the chosen units (e.g.
is the concentration in the chosen units (e.g. 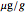 ),
), 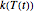 is the rate constant at the momentary temperature in °C, and
is the rate constant at the momentary temperature in °C, and  is the reaction's kinetic order. The initial condition is
is the reaction's kinetic order. The initial condition is 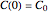 , with concentration in the chosen units. For simplicity, assign
, with concentration in the chosen units. For simplicity, assign 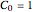 . The temperature dependence of the rate constant usually follows the exponential model
. The temperature dependence of the rate constant usually follows the exponential model 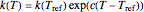 , where
, where  is a reference temperature and
is a reference temperature and  is a characteristic constant having units
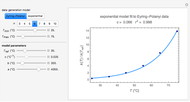
is a characteristic constant having units 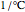 . It has been demonstrated that this simpler model can be used interchangeably with the Arrhenius equation [1, 2, 3, 4].
. It has been demonstrated that this simpler model can be used interchangeably with the Arrhenius equation [1, 2, 3, 4].
The familiar isothermal solutions of the rate equation where 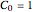 are: for
are: for  ,
,  , for
, for  ,
, 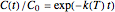 , and for
, and for 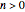 and
and 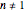 ,
, 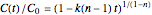 . Where
. Where  and
and 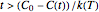 , the concentration ratio becomes negative and is therefore set equal to zero. For
, the concentration ratio becomes negative and is therefore set equal to zero. For 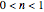 and
and 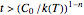 , the concentration ratio becomes a complex number and thus is also set to zero beyond this point.
, the concentration ratio becomes a complex number and thus is also set to zero beyond this point.
Under nonisothermal conditions of the kind encountered in uncontrolled storage, the rate equation has no analytical solution, but it can be solved numerically with Mathematica's NDSolve function to produce and plot the degradation curve.
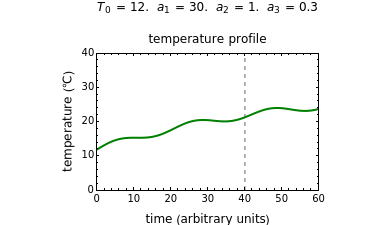
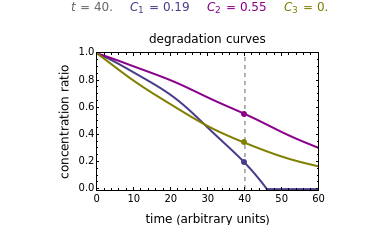
In this Demonstration you can simultaneously generate and follow the isothermal degradation curves of three hypothetical nutrients at your chosen temperature. You can also simultaneously generate and follow degradation curves of three hypothetical nutrients at three chosen nonisothermal temperature histories. Use the sliders to vary their degradation kinetic orders 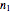 ,
, 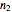 , and
, and 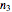 , reference temperatures
, reference temperatures 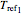 ,
, 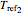 , and
, and 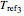 , the corresponding rate constants
, the corresponding rate constants 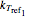 ,
, 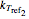 , and
, and 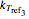 , characteristic constants
, characteristic constants 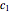 ,
, 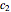 , and
, and 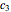 , and the plots’ axes limits. The program plots the temperature profile and the three degradation curves that correspond to the kinetic and plot parameters’ settings. Move the
, and the plots’ axes limits. The program plots the temperature profile and the three degradation curves that correspond to the kinetic and plot parameters’ settings. Move the  slider to calculate and display the numerical values of the three concentration ratios.
slider to calculate and display the numerical values of the three concentration ratios.
The Demonstration helps one to visualize and compare how the degradation of nutrients that follow different kinetic orders, or the same order but with different kinetic parameters, can be affected by the temperature history of their storage. It can also be used to identify combinations of kinetic parameters that will produce similar degradation patterns under the same storage conditions.
Not all parameters allowed by the Demonstration necessarily have realistic counterparts in foods, fortified foods, or multivitamin food supplements.
References
[1] M. Peleg, M. D. Normand, and M. G. Corradini, "The Arrhenius Equation Revisited," Critical Reviews in Food Science and Nutrition, 52(9), 2012 pp. 830–851. doi:10.1080/10408398.2012.667460.
[2] M. Peleg, M. D. Normand, and A. D. Kim, "Estimating Thermal Degradation Kinetics Parameters from the Endpoints of Non-isothermal Heat Processes or Storage," Food Research International, 66, 2014 pp. 313–324. doi:10.1016/j.foodres.2014.10.003.
[3] M. Peleg, A. D. Kim, and M. D. Normand, "Predicting Anthocyanins' Isothermal and Non-isothermal Degradation with the Endpoints Method," Food Chemistry, 187, 2015 pp. 537–544. doi:10.1016/j.foodchem.2015.04.091.
[4] M. Peleg and M. D. Normand, "Predicting Chemical Degradation During Storage from Two Successive Concentration Ratios: Theoretical Investigation," Food Research International, 75, 2015 pp. 174–181. doi:10.1016/j.foodres.2015.06.005.
Permanent Citation