Extracting Fixed-Order Degradation Kinetics by the Endpoints Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Consider a degradation reaction that follows fixed-order kinetics,  , in which the temperature dependence of the rate constant is characterized by a two-parameter exponential model. In principle, both
, in which the temperature dependence of the rate constant is characterized by a two-parameter exponential model. In principle, both  and the two parameters can be extracted from the concentration of the decaying reactant at the end of three dynamic processes whose temperature history has been accurately recorded. This is done by numerically solving the rate equations for the three processes, with
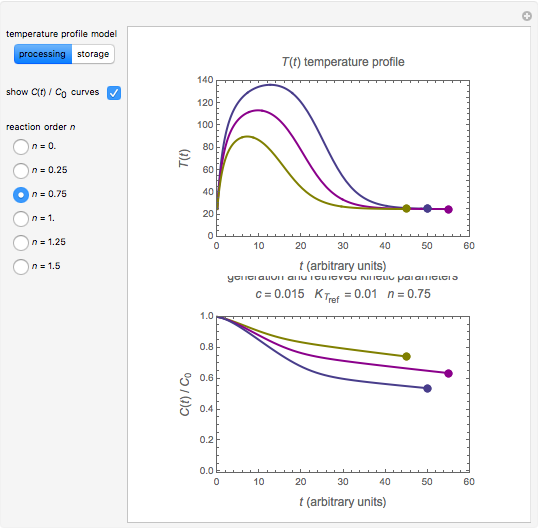
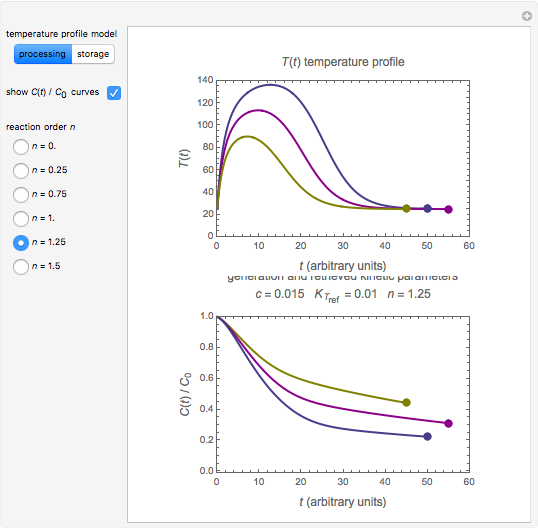
and the two parameters can be extracted from the concentration of the decaying reactant at the end of three dynamic processes whose temperature history has been accurately recorded. This is done by numerically solving the rate equations for the three processes, with  and the temperature-dependence parameters being three unknowns. The concept is demonstrated by generating three endpoints for three histories representing thermal treatments of foods, or storage under fluctuating temperatures, and retrieving the generation parameters.
and the temperature-dependence parameters being three unknowns. The concept is demonstrated by generating three endpoints for three histories representing thermal treatments of foods, or storage under fluctuating temperatures, and retrieving the generation parameters.
Contributed by: Mark D. Normand and Micha Peleg (December 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Determining a degradation reaction's kinetic order and its rate constant's temperature dependence has been traditionally done by recording the degradation curve at several constant temperatures. For logistic considerations, and in some cases technical reasons, recording the entire degradation curve might not be a feasible or viable option. Difficulty in retrieving a sample and/or eliminating the come-up and cooling times are good examples. Both problems would be avoided if one could determine the kinetic parameters from the endpoints of nonisothermal treatments or processes. Theoretically, at least, this is possible [1], and the objective of this Demonstration is to present the concept's application with simulated degradation reactions that follow fixed-order kinetics  , that is, where the diminishing concentration
, that is, where the diminishing concentration 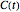 is described by the rate equation
is described by the rate equation 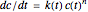 ,
, 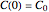 , where
, where 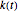 is the temperature rate constant, whose units are in
is the temperature rate constant, whose units are in 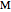 per unit time for
per unit time for  ,
, 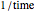 for
for  and
and 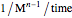 for
for 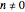 or
or 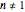 .
. 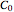 is the initial measured or known reactant's concentration.
is the initial measured or known reactant's concentration.
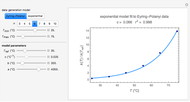
For simplicity, assume that the temperature dependence of the rate constant 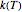 follows the exponential model
follows the exponential model 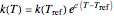 , which in many cases can be used interchangeably with the Arrhenius or Eyring–Polyanyi models [2, 3].
, which in many cases can be used interchangeably with the Arrhenius or Eyring–Polyanyi models [2, 3].
Consider three temperature histories, 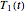 ,
, 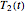 , and
, and 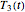 , whether of a heat treatment or storage, ending at
, whether of a heat treatment or storage, ending at 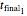 ,
, 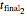 , and
, and 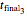 with a corresponding (measured)
with a corresponding (measured) 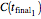 ,
, 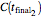 , and
, and 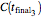 . These values are also the solutions of the three rate equations, that is, for
. These values are also the solutions of the three rate equations, that is, for 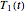 ,
, 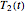 , and
, and 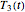 , which if solved simultaneously render the three unknowns, namely,
, which if solved simultaneously render the three unknowns, namely,  ,
,  , and
, and 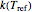 . Because the numerical solution of the three equations is extremely sensitive to the initial guesses, we have reduced the problem to solving two equations with two unknowns to extract
. Because the numerical solution of the three equations is extremely sensitive to the initial guesses, we have reduced the problem to solving two equations with two unknowns to extract  and
and 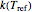 for
for  values that change iteratively by predetermined increments or decrements. At each iteration, the current values of
values that change iteratively by predetermined increments or decrements. At each iteration, the current values of  and the corresponding
and the corresponding  and
and 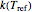 are used to calculate the final concentration at the end of the third treatment. Once this value falls within a chosen tolerance, the iterations stop and the triplet
are used to calculate the final concentration at the end of the third treatment. Once this value falls within a chosen tolerance, the iterations stop and the triplet  ,
,  , and
, and 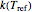 is considered the estimate of the reaction's kinetic parameters.
is considered the estimate of the reaction's kinetic parameters.
The rate equation of a degradation process of an arbitrary order  ,
, 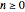 , and
, and 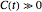 can be written in the form
can be written in the form
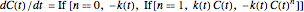 .
.
(In the general case where 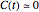 , there are parameter combinations that might render negative or complex concentrations. In such cases, disallowed in this Demonstration, additional If statements to avoid such situations may be necessary.)
, there are parameter combinations that might render negative or complex concentrations. In such cases, disallowed in this Demonstration, additional If statements to avoid such situations may be necessary.)
For the method to work, the final times chosen ought to be such that none of the corresponding concentrations are zero or close to zero.
Because of the method's extreme sensitivity to even slight scatter or errors in the 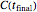 values, application of the method to real data may require adjustment of the initial guesses and/or the tolerance level. The method's reliability increases if the calculations are repeated with different permutations of the triplets and averaging the results, or better still, using more than three profiles, in which case outliers could be identified by statistical criteria and removed [4]. The method can also be applied to the endpoints of isothermal degradation curves, which are a special case where
values, application of the method to real data may require adjustment of the initial guesses and/or the tolerance level. The method's reliability increases if the calculations are repeated with different permutations of the triplets and averaging the results, or better still, using more than three profiles, in which case outliers could be identified by statistical criteria and removed [4]. The method can also be applied to the endpoints of isothermal degradation curves, which are a special case where 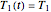 ,
, 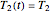 , and
, and 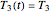 . If, in the method's application to experimental endpoints, the iterations fail to converge or yield absurd parameter values such as a negative
. If, in the method's application to experimental endpoints, the iterations fail to converge or yield absurd parameter values such as a negative  , one should suspect that either the reaction does not follow fixed-order kinetics or that the experimental scatter is too large.
, one should suspect that either the reaction does not follow fixed-order kinetics or that the experimental scatter is too large.
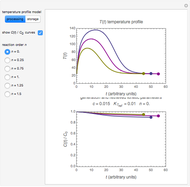
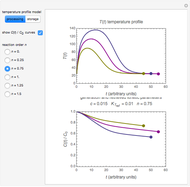
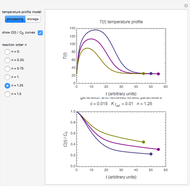
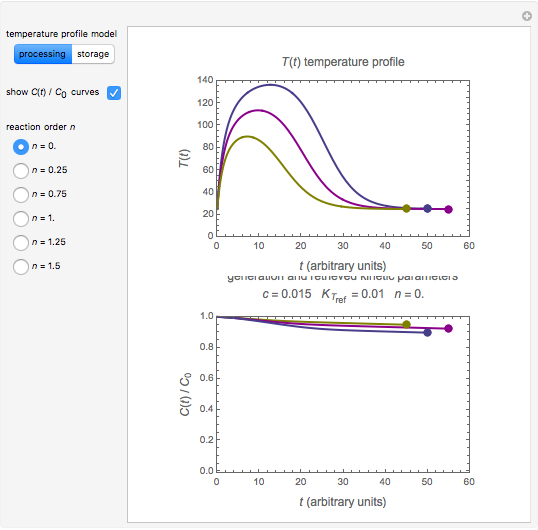
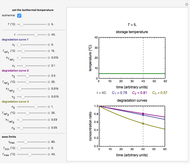
In this Demonstration, the choice is between fixed heating and cooling profiles and fluctuating storage temperatures, selected by a setter bar. Also fixed are the values of  and
and 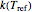 . To generate the triplet of endpoints, select a value of
. To generate the triplet of endpoints, select a value of  , and to show the calculated degradation curves, check the "show
, and to show the calculated degradation curves, check the "show 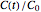 curves" checkbox. The generation and calculated parameters retrieved using the method will be displayed above the plot of the three degradation curves.
curves" checkbox. The generation and calculated parameters retrieved using the method will be displayed above the plot of the three degradation curves.
References
[1] M. Peleg, M. D. Normand, M. G. Corradini, A. J. van Asselt, P. de Jong, and P. F. ter Steeg, "Estimating the Heat Resistance Parameters of Bacterial Spores from Their Survival Ratios at the End of UHT and Other Heat Treatments," Critical Reviews in Food Science and Nutrition, 48(7), 2008 pp. 634–648. doi:10.1080/10408390701724371.
[2] M. Peleg, M. D. Normand, and M. G. Corradini, "The Arrhenius Equation Revisited," Critical Reviews in Food Science and Nutrition, 52(9), 2012 pp. 830–851. doi:10.1080/10408398.2012.667460.
[3] C. S. Barsa, M. D. Normand, and M. Peleg, "On Models of the Temperature Effect on the Rate of Chemical Reactions and Biological Processes in Foods," Food Engineering Reviews, 4, 2012 pp. 191–202.
[4] M. G. Corradini, M. D. Normand, and M. Peleg, "Prediction of an Organism's Inactivation Patterns from Three Single Survival Ratios Determined at the End of Three Non-Isothermal Heat Treatments," International Journal of Food Microbiology, 126, 2008 pp. 98–111.
Permanent Citation